题目内容
18.先化简,再求值:$\frac{x-3}{x-2}÷(x+2-\frac{5}{x-2})$,其中x=-$\frac{1}{2}$.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{x-3}{x-2}$÷$\frac{{x}^{2}-9}{x-2}$
=$\frac{x-3}{x-2}$•$\frac{x-2}{(x+3)(x-3)}$
=$\frac{1}{x+3}$,
当x=-$\frac{1}{2}$时,原式=$\frac{1}{-\frac{1}{2}+3}$=$\frac{2}{5}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
6.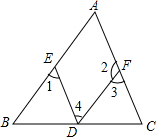 如图,在下列给出的条件中,不能判定AB∥DF的是( )
如图,在下列给出的条件中,不能判定AB∥DF的是( )
 如图,在下列给出的条件中,不能判定AB∥DF的是( )
如图,在下列给出的条件中,不能判定AB∥DF的是( )| A. | ∠A+∠2=180° | B. | ∠1=∠A | C. | ∠1=∠4 | D. | ∠A=∠3 |
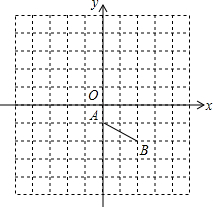 如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在格线上.线段AB的两个端点也在格点上.
如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在格线上.线段AB的两个端点也在格点上. (1)解不等式组:$\left\{\begin{array}{l}{5-x>3}\\{\frac{x}{2}-\frac{2x-1}{3}-1≤0}\end{array}\right.$
(1)解不等式组:$\left\{\begin{array}{l}{5-x>3}\\{\frac{x}{2}-\frac{2x-1}{3}-1≤0}\end{array}\right.$
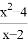 的值为零,那么x=__________.
的值为零,那么x=__________.