题目内容
学校门口经常有小贩搞摸奖活动,某小贩在一只黑色的口袋里装有只有颜色不同的30只小球,其中红球1只,黄球2只,绿球10只,其余为白球,搅拌均匀后,每2元摸1个球,摸到红球奖励8元,摸到黄球奖励5元,摸到绿球奖励2元.
(1)如果花2元摸1个球,那么摸不到奖的概率是多少?
(2)如果花4元同时摸2个球,那么获得10元奖品的概率是多少?
(1)如果花2元摸1个球,那么摸不到奖的概率是多少?
(2)如果花4元同时摸2个球,那么获得10元奖品的概率是多少?
考点:列表法与树状图法
专题:
分析:(1)由红球1只,黄球2只,绿球10只,其余为白球,搅拌均匀后,每2元摸1个球,摸到红球奖励8元,摸到黄球奖励5元,摸到绿球奖励2元,直接利用概率公式求解即可求得答案;
(2)由乘法公式可得:花4元同时摸2个球,等可能的结果共有:30×29=870(种),且获得10元奖品的有22种情况,然后利用概率公式求解即可求得答案.
(2)由乘法公式可得:花4元同时摸2个球,等可能的结果共有:30×29=870(种),且获得10元奖品的有22种情况,然后利用概率公式求解即可求得答案.
解答:解:(1)∵红球1只,黄球2只,绿球10只,其余为白球,搅拌均匀后,每2元摸1个球,摸到红球奖励8元,摸到黄球奖励5元,摸到绿球奖励2元,
∴如果花2元摸1个球,那么摸不到奖的概率是:
=
;
(2)∵花4元同时摸2个球,等可能的结果共有:30×29=870(种),且获得10元奖品的有22种情况,
∴如果花4元同时摸2个球,那么获得10元奖品的概率是:
=
.
∴如果花2元摸1个球,那么摸不到奖的概率是:
| 30-1-2-10 |
| 30 |
| 17 |
| 30 |
(2)∵花4元同时摸2个球,等可能的结果共有:30×29=870(种),且获得10元奖品的有22种情况,
∴如果花4元同时摸2个球,那么获得10元奖品的概率是:
| 22 |
| 870 |
| 11 |
| 435 |
点评:此题考查了列举法求概率的知识.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 如图,已知△ABM≌△CDN,∠A=50°,则∠NCB等于( )
如图,已知△ABM≌△CDN,∠A=50°,则∠NCB等于( )| A、30° | B、40° |
| C、50° | D、60° |
在平面直角坐标系中,对于平面内一点(m,n)规定以下两种变换,
①f(m,n)=(m,-n),如f(2,1)=(2,-1);
②g(m,n)=(-m,-n),如g(2,1)=(-2,-1).
按照以上变换,则经过点f[g(3,4)],点g[f(-3,2)]的直线方程为( )
①f(m,n)=(m,-n),如f(2,1)=(2,-1);
②g(m,n)=(-m,-n),如g(2,1)=(-2,-1).
按照以上变换,则经过点f[g(3,4)],点g[f(-3,2)]的直线方程为( )
A、y=-
| ||
B、y=
| ||
C、y=-
| ||
D、y=
|
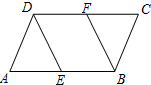 如图,在平行四边形ABCD中,AE=CF.求证:
如图,在平行四边形ABCD中,AE=CF.求证: 如图,数轴上有A、B、C、D、O五个点,点O为原点,点C在数轴上表示的数是5,线段CD的长度为4个单位,线段AB的长度为2个单位,且B、C两点之间的距离为11个单位,请解答下列问题:
如图,数轴上有A、B、C、D、O五个点,点O为原点,点C在数轴上表示的数是5,线段CD的长度为4个单位,线段AB的长度为2个单位,且B、C两点之间的距离为11个单位,请解答下列问题: 已知一次函数y=ax+c的图象如图所示,那么一次函数y=cx+a的大致图象是( )
已知一次函数y=ax+c的图象如图所示,那么一次函数y=cx+a的大致图象是( )


