题目内容
2.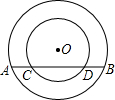 已知在以点O为圆心的两个同心圆中,大圆的弦交小圆于点C、D
已知在以点O为圆心的两个同心圆中,大圆的弦交小圆于点C、D(1)求证:AC=BD;
(2)若大圆的半径r=8,小圆的半径r=6,且圆心O到直线AB的距离为4,求AC的长.
分析 (1)过O作OE⊥AB,根据垂径定理得到AE=BE,CE=DE,从而得到AC=BD;
(2)连接OC,OA,根据OE⊥AB且OE⊥CD可得OE=6,CE=DE,再根据勾股定理求出CE及AE的长,进而可得出结论.
解答 (1)证明:作OE⊥AB,则AE=BE,CE=DE,
故BE-DE=AE-CE;
即AC=BD;
(2)解:连接OC,OA,
∵OE⊥AB且OE⊥CD,
∴OE=4,CE=DE,
∴DE=CE=$\sqrt{O{C}^{2}-O{E}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
AE=$\sqrt{O{A}^{2}-O{E}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴AC=AE-CE=4$\sqrt{3}$-2$\sqrt{5}$.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
17.下列各数中,是无理数的是( )
| A. | $\sqrt{2}$ | B. | $\root{3}{8}$ | C. | $\sqrt{16}$ | D. | $\frac{1}{3}$ |
7.四舍五入法按要求对0.05019分别取近似值,其中错误的是( )
| A. | 0.1(精确到0.1) | B. | 0.05(精确到百分位) | ||
| C. | 0.050(精确到百分位) | D. | 0.0502(精确到0.0001) |
14.2016年,我国约有9400000人参加高考,将9400000用科学记数法表示为( )
| A. | 9.4×105 | B. | 9.4×106 | C. | 0.94×106 | D. | 94×104 |