题目内容
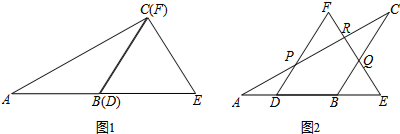
5.如图1,已知等腰三角形ABC的顶角∠ABC=120°,等边三角形DEF的边DE=AB=1,若△DEF不动,将△ABC从BC与DF重合的位置开始(如图1),沿直线DE方向平移,且保持AB与DE在同一直线上,直到点A与点E重合为止.(1)图2所示的是,在平移过程中,点B在DE上时,△ABC的AC、BC两边分别与△DEF的DF、EF两边交于点P,Q,R,求证:DB=PF;
(2)设平移距离DB=x,△ABC和△DEF重叠部分的面积为S,求S与x的函数关系式.
分析 (1)首先根据题意得到AD=DP,结合AB=DE=DF=1,即可证明DB=PF;
(2)当0<x<1时,用x表示出△PFR和△BQE的面积,利用△DEF的面积减去△PFR和△BQE的面积即可得到S与x的函数关系式;当1≤x<2时,用x表示出△AER的面积即可.
解答 (1)证明:∵∠FDB=60°,∠A=30°,
∴∠APD=30°,
∴AD=DP,
∵AB=DE=DF,
∴AD+DB=DP+PF,
∴DB=PF;
(2)当0<x<1时,
∵DB=x,
∴PF=x,
∵∠A=∠APD=30°,
∴∠FPR=30°,
∵∠F=60°
∴∠FRP=90°,
∴PR=$\frac{\sqrt{3}}{2}$x,
∴S△PFR=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$x2=$\frac{\sqrt{3}}{8}$x2,
∴S△BQE=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$(1-x)2=$\frac{\sqrt{3}}{4}$(1-x)2,
∴△ABC和△DEF重叠部分的面积为S=$\frac{\sqrt{3}}{4}$-$\frac{\sqrt{3}}{8}$x2-$\frac{\sqrt{3}}{4}$(1-x)2=-$\frac{3\sqrt{3}}{8}$x2+$\frac{\sqrt{3}}{2}$x(0<x<1),
当1≤x<2时,如图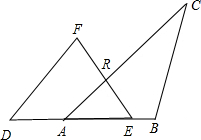
BD=x,AD=x-1,AE=2-x,
∵∠CAB=30°,∠AER=60°,
∴∠ARE=90°,
∴RE=1-$\frac{1}{2}$x,AR=$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x,
∴S△AER=$\frac{1}{2}$(1-$\frac{1}{2}$x)($\sqrt{3}$-$\frac{\sqrt{3}}{2}$x)=$\frac{\sqrt{3}}{8}$x2-$\frac{\sqrt{3}}{2}$x+$\frac{\sqrt{3}}{2}$,
综上S=$\left\{\begin{array}{l}{-\frac{3\sqrt{3}{x}^{2}}{8}+\frac{\sqrt{3}}{2}x(0<x<1)}\\{\frac{\sqrt{3}}{8}{x}^{2}-\frac{\sqrt{3}}{2}x+\frac{\sqrt{3}}{2}(1≤x<2)}\end{array}\right.$.
点评 本题主要考查了几何变换综合题,此题涉及到等腰三角形的性质、等边三角形的性质、平移的性质以及三角形面积的计算等知识,此题难度不大,解答(2)问需要分区间讨论.

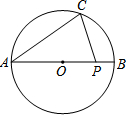 如图,AB是⊙O的直径,点C在圆周上,点P是线段OB上任意一点,连结AC、CP.若∠BAC=35°,则∠APC的度数不可能是( )
如图,AB是⊙O的直径,点C在圆周上,点P是线段OB上任意一点,连结AC、CP.若∠BAC=35°,则∠APC的度数不可能是( )| A. | 90° | B. | 75° | C. | 60° | D. | 50° |
| A. | 三个内角之比为5:6:1 | B. | 一边上的中线等于这一边的一半 | ||
| C. | 三边之比为20、21、29 | D. | 三边之比为1.5:2:3 |
 如图,点D在线段AB上,且D是线段AB的中点,BD=4,则线段AB的长为( )
如图,点D在线段AB上,且D是线段AB的中点,BD=4,则线段AB的长为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
| A. | a≠-1 | B. | a≠0 | C. | a≠1 | D. | a=-1 |
| A. | a<-1 | B. | a>-1 | C. | a<1 | D. | a<0 |
 已知直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE,∠1=30°,求∠BOF和∠DOF的度数.
已知直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE,∠1=30°,求∠BOF和∠DOF的度数. 解不等式3(x-2)≤4x-3,并把它的解集在数轴上表示出来.
解不等式3(x-2)≤4x-3,并把它的解集在数轴上表示出来.