��Ŀ����
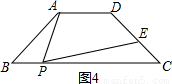
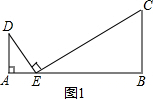 ��1�����ԣ���ͼ����֪A��E��B������ͬһֱ���ϣ��ҡ�A=��B=��DEC=90�㣬
��1�����ԣ���ͼ����֪A��E��B������ͬһֱ���ϣ��ҡ�A=��B=��DEC=90�㣬��֤��AE•BE=AD•BC��
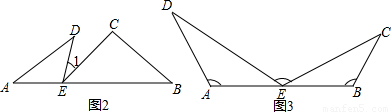
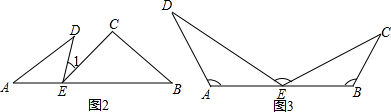
��2��һλͬѧ�ڳ�����������֣���ͼ2��ͼ3��ֻҪA��E��B������ͬһֱ���ϣ��ҡ�A=��B=��DEC����1���н����ܳ�������ͬ������ѡ������֮һ˵�����ɣ�
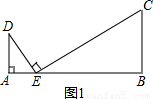
��3�����ã���ͼ���ı���ABCD�ǵ������Σ�AD��BC��AB=4��BC=9��PΪBC����һ���㣨�����B��C
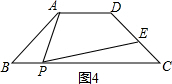 �غϣ�������AP������P��PE��CD�ڵ�E��ʹ�á�APE=��ABC����BPΪ��ֵʱ����EΪCD���е㣮
�غϣ�������AP������P��PE��CD�ڵ�E��ʹ�á�APE=��ABC����BPΪ��ֵʱ����EΪCD���е㣮
��������1��������֪�ó���D=��CEB���Լ���A=��B���ɵó���ADE�ס�BEC�����ɵó��𰸣�
��2��������֪�ó���D=��CEB�����������ADE�ס�BEC�����ɵó�
=
��
��3�������EΪCD���е㣬���á�ABP�ס�PCE���ó�����ʽ������ɣ�
��2��������֪�ó���D=��CEB�����������ADE�ס�BEC�����ɵó�
| AE |
| BC |
| AD |
| BE |
��3�������EΪCD���е㣬���á�ABP�ס�PCE���ó�����ʽ������ɣ�
�����1��֤�����ߡ�A=��B=��DEC=90�㣬
���DEA+��CEB=90�㣬
�ߡ�DEA+��D=90�㣬
���D=��CEB��
���ADE�ס�BEC��
��
=
��
��AE•BE=AD•BC��
��2��֤�����ߡ�A=��B=��DEC��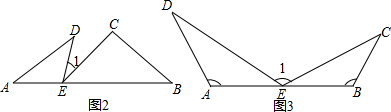
��A+��D=��1+��CEB��
���D=��CEB��
���ADE�ס�BEC��
��
=
��
��AE•BE=AD•BC��
��3���⣺���ı���ABCD�ǵ������Σ�AD��BC����APE=��ABC
���B=��C����B+��BAP=��APE+��EPC��
���BAP=��EPC��
���ABP�ס�PCE��
��
=
��
��AB=4��BC=9����EΪCD���е㣬
��CE=2������BP=x��
��
=
��
��x2-9x+8=0��
��ã�x1=1��x2=8��
�൱BPΪ1��8ʱ����EΪCD���е㣮
���DEA+��CEB=90�㣬

�ߡ�DEA+��D=90�㣬
���D=��CEB��
���ADE�ס�BEC��
��
| AE |
| BC |
| AD |
| BE |
��AE•BE=AD•BC��
��2��֤�����ߡ�A=��B=��DEC��

��A+��D=��1+��CEB��
���D=��CEB��
���ADE�ס�BEC��
��
| AE |
| BC |
| AD |
| BE |
��AE•BE=AD•BC��
��3���⣺���ı���ABCD�ǵ������Σ�AD��BC����APE=��ABC

���B=��C����B+��BAP=��APE+��EPC��
���BAP=��EPC��
���ABP�ס�PCE��
��
| AB |
| PC |
| BP |
| CE |
��AB=4��BC=9����EΪCD���е㣬
��CE=2������BP=x��
��
| 4 |
| 9-x |
| x |
| 2 |
��x2-9x+8=0��
��ã�x1=1��x2=8��
�൱BPΪ1��8ʱ����EΪCD���е㣮
������������Ҫ���������������ε��������ж������������ε��ж��dz��нο�����ص�ͬѧ��Ӧ�ص����գ�

��ϰ��ϵ�д�
�����Ŀ


 ��1�����ԣ���ͼ����֪A��E��B������ͬһֱ���ϣ��ҡ�A=��B=��DEC=90�㣬
��1�����ԣ���ͼ����֪A��E��B������ͬһֱ���ϣ��ҡ�A=��B=��DEC=90�㣬
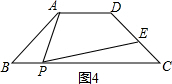 �غϣ�������AP������P��PE��CD�ڵ�E��ʹ�á�APE=��ABC����BPΪ��ֵʱ����EΪCD���е㣮
�غϣ�������AP������P��PE��CD�ڵ�E��ʹ�á�APE=��ABC����BPΪ��ֵʱ����EΪCD���е㣮