题目内容
5.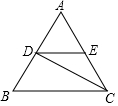 在等边三角形ABC中,边长为2,CD平分∠ACB,交AB于点D,DE∥BC,则△ADE的周长为( )
在等边三角形ABC中,边长为2,CD平分∠ACB,交AB于点D,DE∥BC,则△ADE的周长为( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 4 |
分析 由平行线的性质可判定△ADE为等边三角形,再由等边三角形的性质可知D为AB中点,可求得AD的长,可求得答案.
解答 解:
∵△ABC为等边三角形,
∴∠B=∠ACB=60°,
∵DE∥BC,
∴∠ADE=∠AED=60°,
∴△ADE为等边三角形,
∵CD平分∠ACB,
∴D为AB中点,
∴AD=$\frac{1}{2}$AB=1,
∴△ADE的周长=3AD=3,
故选C.
点评 本题主要考查等边三角形的判定和性质,掌握等边三角形的三边相等及“三线合一”是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.某日的最高气温为8℃,最低气温为-4℃,则这一天的最高气温比最低气温高( )
| A. | -12℃ | B. | -6℃ | C. | 6℃ | D. | 12℃ |
16.下列方程一定是一元二次方程的是( )
| A. | x2+$\frac{2}{x}$-1=0 | B. | 2x2-y-3=0 | C. | ax2-x+2=0 | D. | 3x2-2x-1=0 |
13.下列方程中,一元二次方程是( )
| A. | x2+$\frac{1}{{x}^{2}}$=0 | B. | (2x-1)(x+2)=1 | C. | ax2+bx=0 | D. | 3x2-2xy-5y2=0 |
20.下列计算正确的是( )
| A. | $\sqrt{6}$+$\sqrt{3}$=3 | B. | 4$\sqrt{2}$-3$\sqrt{2}$=1 | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{(-2)^{2}}$=2 |
10.五个有理数的积是负数,这五个数中负因数个数是( )
| A. | 1个 | B. | 3个 | C. | 5个 | D. | 都有可能 |
17.下列说法中正确的是( )
| A. | 正数和负数统称为有理数 | B. | 0既不是整数,又不是分数 | ||
| C. | 0是最小的正数 | D. | 整数和分数统称有理数 |
14.下列各点中,在反比例函数y=$\frac{3}{x}$图象上的是( )
| A. | (3,1) | B. | (-3,1) | C. | (3,$\frac{1}{3}$) | D. | ($\frac{1}{3}$,3) |
15.给出下列各数:0,π,-$\frac{22}{7}$,3.14,-10,其中有理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |