题目内容
11.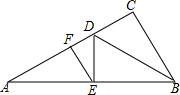 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,DE⊥AB于E,EF∥BC交AC于F.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,DE⊥AB于E,EF∥BC交AC于F.(L)求证:△EDF∽△ADE;
(2)猜想:线段DC,DF、DA之间存在什么关系?并说明理由.
分析 (1)利用垂直的定义和平行线的性质可证明∠DFE=∠DEA=90°,则利用相似三角形的判定方法可判断△EDF∽△ADE;
(2)由于△EDF∽△ADE,则利用相似比可得到DE2=DF•DA,再利用角平分线的性质定理得到DE=DC,从而得到线段DC,DF、DA之间的关系.
解答 (1)证明:∵DE⊥AB,
∴∠AED=90°,
∵EF∥BC,
∴∠AFE=∠C=90°,
∴∠DFE=∠DEA,
而∠FDE=∠EDA,
∴△EDF∽△ADE;
(2)解:DC2=DF•DA.理由如下:
∵△EDF∽△ADE,
∴DE:DA=DF:DE,
即DE2=DF•DA,
∵BD平分∠ABC,DE⊥AB,DC⊥BC,
∴DE=DC,
∴DC2=DF•DA.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.解决本题的关键是利用相似三角形比得到DE、DF、DA的关系.

练习册系列答案
相关题目
1.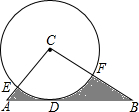 如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
 如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )| A. | $\frac{32}{3}\sqrt{3}-4π$ | B. | $\frac{32}{3}\sqrt{3}-2π$ | C. | 16-4π | D. | 16-2π |
2.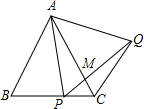 如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
①AB∥CQ;②∠ACQ=60°;③AP2=AM•AC;④若BP=PC,则PQ⊥AC.
 如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )①AB∥CQ;②∠ACQ=60°;③AP2=AM•AC;④若BP=PC,则PQ⊥AC.
| A. | 只有①② | B. | 只有①③ | C. | 只有①②③ | D. | ①②③④ |
6.在平面直角坐标系中,点P(-3,2)关于直线y=x对称点的坐标是( )
| A. | (-3,-2) | B. | (3,2) | C. | (2,-3) | D. | (3,-2) |
3.已知:2m+3n=5,则4m•8n=( )
| A. | 16 | B. | 25 | C. | 32 | D. | 64 |
 已知:△ABC
已知:△ABC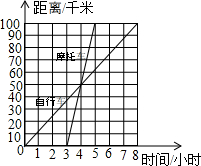 如图所示,是一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象,两地间的距离是100千米,请根据图象填空:
如图所示,是一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象,两地间的距离是100千米,请根据图象填空: