题目内容
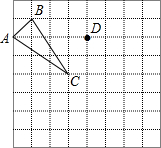 如图,△ABC在正方形网格中(每个小方格都是边长为1的正方形),请解答下列问题:
如图,△ABC在正方形网格中(每个小方格都是边长为1的正方形),请解答下列问题:(1)将△ABC沿某个方向平移后得△EDF,点B的对应点为点D(如图),请画出EDF;
(2)连接BE、BD,求四边形BEFD的面积.
分析:(1)根据网格结构找出点A、C平移后的对应点E、F的位置,再与点D顺次连接即可;
(2)用构成四边形的两个三角形所在的矩形的面积减去四周直角三角形的面积再减去公共边DE所在的正方形的面积,列式计算即可得解.
(2)用构成四边形的两个三角形所在的矩形的面积减去四周直角三角形的面积再减去公共边DE所在的正方形的面积,列式计算即可得解.
解答: 解:(1)△EDF如图所示;
解:(1)△EDF如图所示;
(2)四边形BEFD的面积=3×2-
×3×1-
×2×2+3×3-
×2×3-
×2×3-12,
=6-1.5-2+9-3-3-1,
=15-10.5,
=4.5.
 解:(1)△EDF如图所示;
解:(1)△EDF如图所示;(2)四边形BEFD的面积=3×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=6-1.5-2+9-3-3-1,
=15-10.5,
=4.5.
点评:本题考查了利用平移变化作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键,(2)要注意DE所在的正方形的面积被重复计算.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目

 如图,△ABC三个顶点都在方格纸的格点上,且点A的坐标为(-2,3).将△ABC沿x轴正方向平移4个单位,再沿y轴的负方向平移3个单位,得到△A′B′C′(A→A′,B→B′,C→C′)
如图,△ABC三个顶点都在方格纸的格点上,且点A的坐标为(-2,3).将△ABC沿x轴正方向平移4个单位,再沿y轴的负方向平移3个单位,得到△A′B′C′(A→A′,B→B′,C→C′) 如图,△ABC的三个顶点坐标分别为A(-1,1)、B(-2,3)、C(-1,3),
如图,△ABC的三个顶点坐标分别为A(-1,1)、B(-2,3)、C(-1,3), 如图将△ABC沿x轴的正方向平移4单位得到△A′B′O′,再绕O′点按顺时针旋转90°得到△A″B″O″,若A的坐标为(-2,3),B点坐标为(-3,0);
如图将△ABC沿x轴的正方向平移4单位得到△A′B′O′,再绕O′点按顺时针旋转90°得到△A″B″O″,若A的坐标为(-2,3),B点坐标为(-3,0);