题目内容
如图,在Rt △ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )
△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )
A. 点B到AO的距离为sin54° B. 点B到AO的距离为tan36°
C. 点A到OC的距离为sin36°sin54° D. 点A到OC的距离为cos36°sin54°


C 解析:在Rt△ABO中,OC∥BA,∠AOC=36°,∴∠BAO=36°,∠OBA=54°,

如图,作BE⊥OC,BO=sin∠BAO·AB=sin36°·AB,而BE=sin ∠BOE·OB,∵AB=1,∴BE=sin 36°sin54°,即点A到OC的距离为sin36°sin54°,故选C.

练习册系列答案
相关题目
 的解是负数,则a的取值范围是( ).
的解是负数,则a的取值范围是( ). B.a<3 C.a≥3 D.a≤
B.a<3 C.a≥3 D.a≤ 的数分别是
的数分别是 和
和 ,且点A,B到原点的距离相等,
,且点A,B到原点的距离相等, 求
求 的值.
的值. =___________.
=___________. ,然后
,然后 在﹣1、
在﹣1、 1、2三个数中任选一个合适的数代入求值.
1、2三个数中任选一个合适的数代入求值.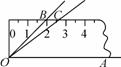

 B.
B. 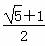 C.
C.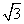 D.2
D.2
 的解集是______.
的解集是______.