题目内容
17.解方程组:$\left\{\begin{array}{l}{6={k}_{1}+{k}_{2}}\\{6=2{k}_{1}+\frac{{k}_{2}}{2}}\end{array}\right.$.分析 方程组整理后,利用加减消元法求出解即可.
解答 解:方程组整理得:$\left\{\begin{array}{l}{{k}_{1}+{k}_{2}=6①}\\{4{k}_{1}+{k}_{2}=12②}\end{array}\right.$,
②-①得:3k1=6,即k1=2,
把k1=2代入①得:k2=4,
则方程组的解为$\left\{\begin{array}{l}{{k}_{1}=2}\\{{k}_{2}=4}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
8.某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表,则棉花纤维长度的数据在8≤x<32这个范围的频率为0.8.
| 棉花纤维长度x | 频数 |
| 0≤x<8 | 1 |
| 8≤x<16 | 2 |
| 16≤x<24 | 8 |
| 24≤x<32 | 6 |
| 32≤x<40 | 3 |
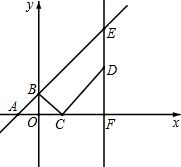 如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于点A,B.点C的坐标为(m,0),将线段BC绕点C顺时针旋转90°,并延长一倍得CD,过点D作x轴的垂线,垂足为F,交直线AB于点E.
如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于点A,B.点C的坐标为(m,0),将线段BC绕点C顺时针旋转90°,并延长一倍得CD,过点D作x轴的垂线,垂足为F,交直线AB于点E.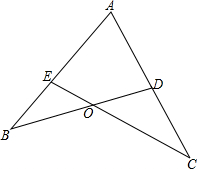 如图,∠A=80°,∠B=∠C,∠DOC=60°,求∠B的度数.
如图,∠A=80°,∠B=∠C,∠DOC=60°,求∠B的度数.