题目内容
20. 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.(1)求证:DE是⊙O的切线;
(2)如果AD=5,AE=4,求⊙O的半径.
分析 (1)连接OD,由AD为角平分线,得到一对角相等,再由OA=OD,得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行可得AE与OD平行,由两直线平行同旁内角互补,得到∠E与∠EDO互补,再由∠E为直角,可得∠EDO为直角,即DE为圆O的切线,得证;
(2)连接BD,由AB为圆O的直径,根据直径所对的圆周角为直角,得到∠ADB为直角,在直角三角形ABD中,利用锐角三角函数定义得到cos∠DAB=$\frac{AD}{AB}$,又在直角三角形AED中,由AE及AD的长,利用锐角三角函数定义求出cos∠EAD的值,由∠EAD=∠DAB,得到cos∠EAD=cos∠DAB,得出cos∠DAB的值,即可求出直径AB的长,进而求得半径长.
解答 (1)证明:连接OD,如图1所示:
∵AD为∠CAB的平分线,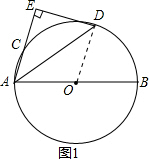
∴∠CAD=∠BAD,
又∵OA=OD,
∴∠BAD=ODA,
∴∠CAD=∠ODA,
∴AC∥OD,
∴∠E+∠EDO=180°,
又∵AE⊥ED,即∠E=90°,
∴∠EDO=90°,
则ED为圆O的切线;
(2)解:连接BD,如图2所示,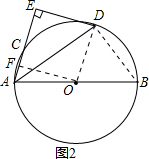 过点A作AF⊥AC,
过点A作AF⊥AC,
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△ABD中,cos∠DAB=$\frac{AD}{AB}$,
在Rt△AED中,AE=4,AD=5,
∴cos∠EAD=$\frac{AE}{AD}$=$\frac{4}{5}$,又∠EAD=∠DAB,
∴cos∠DAB=cos∠EAD=$\frac{AD}{AB}$=$\frac{4}{5}$,
则AB=$\frac{5}{4}$AD=$\frac{25}{4}$,即圆的直径为$\frac{25}{4}$,
∴半径AO=$\frac{25}{8}$.
点评 此题考查了切线的判定,圆周角定理,勾股定理,平行线的判定与性质,以及锐角三角函数定义,切线的证明方法有两种:有点连接证垂直;无点作垂线证明垂线段等于圆的半径.

| A. | 3$\sqrt{3}$-$\sqrt{3}$=2$\sqrt{3}$ | B. | a0=1 | C. | -2+|-2|=0 | D. | (-3)-2=$\frac{1}{9}$ |
| A. | 调查2017年春节晚会的收视率 | |
| B. | 调查重庆全市市民春节期间外出旅游人数 | |
| C. | 调查全国初三学生的视力情况 | |
| D. | 调查某航班的旅客是否携带了违禁物品 |
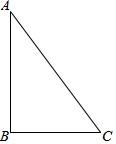 实践操作:如图,在Rt△ABC中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):
实践操作:如图,在Rt△ABC中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法): 如图,给出下列四组条件:
如图,给出下列四组条件: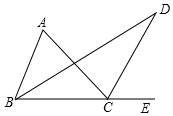 在△ABC中,∠ABC的平分线与在∠ACE的平分线相交于点D.已知∠ABC=70°,∠ACB=30°,求∠A和∠D的度数.
在△ABC中,∠ABC的平分线与在∠ACE的平分线相交于点D.已知∠ABC=70°,∠ACB=30°,求∠A和∠D的度数.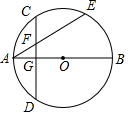 如图,AB是⊙O的直径,点C是弧AE的中点,过点C作CD⊥AB,垂足为点G,AE交CD于点G.
如图,AB是⊙O的直径,点C是弧AE的中点,过点C作CD⊥AB,垂足为点G,AE交CD于点G.