题目内容
15.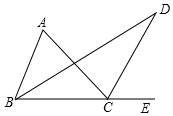 在△ABC中,∠ABC的平分线与在∠ACE的平分线相交于点D.已知∠ABC=70°,∠ACB=30°,求∠A和∠D的度数.
在△ABC中,∠ABC的平分线与在∠ACE的平分线相交于点D.已知∠ABC=70°,∠ACB=30°,求∠A和∠D的度数.
分析 根据三角形内角和定理,已知∠ABC=70°,∠ACB=30°,易求∠A,根据角平分线定义和外角的性质即可求得∠D度数.
解答 解:在△ABC中,∠ABC=70°,∠ACB=30°,
∴∠A=180°-∠ABC-∠ACB=80°,
∵BD为∠ABC,CD为∠ACE的角平分线,
∴∠DBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×70°=35°,
∠ACD=$\frac{1}{2}$(180°-∠ACB)=$\frac{1}{2}$×150°=75°,
∴∠D=180°-∠DBC-∠ACB-∠ACD=180°-35°-30°-75°=40°,
∴∠A=80°,∠D=40°.
点评 本题考查了三角形内角和定理以及角平分线定义,外角的性质,熟练掌握三角形的内角和和外角的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.如果代数式8y2-4y+5的值是13,那么代数式2y2-y+1的值等于( )
| A. | 2 | B. | 3 | C. | -2 | D. | 4 |
10.下列各对数中,互为相反数的是( )
| A. | +(-2)和-2 | B. | -(-2)和-|-2| | C. | -(-2)和|-2| | D. | -(-2)和+(+2) |
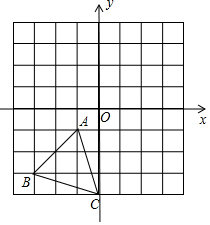
 如图,在△ABC中,AB=6,BC=8,AC=4,D、E、F分别为BC、AC、AB中点,连接DE、FE,则四边形BDEF的周长是14.
如图,在△ABC中,AB=6,BC=8,AC=4,D、E、F分别为BC、AC、AB中点,连接DE、FE,则四边形BDEF的周长是14. 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.