题目内容
10.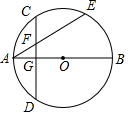 如图,AB是⊙O的直径,点C是弧AE的中点,过点C作CD⊥AB,垂足为点G,AE交CD于点G.
如图,AB是⊙O的直径,点C是弧AE的中点,过点C作CD⊥AB,垂足为点G,AE交CD于点G.(1)求证:AF=CF;
(2)若tan∠BAE=$\frac{3}{4}$,AE=8,求AF的长.
分析 (1)首先连接AC,由垂径定理可得$\widehat{AC}$=$\widehat{AD}$,又由点C是弧AE的中点,可得$\widehat{CE}$=$\widehat{AD}$,继而证得∠ACD=∠CAE,则可证得结论;
(2)由tan∠BAE=$\frac{3}{4}$,易得FG=3x,AG=4x,CF=AF=5x,即可求得CD=16x,然后证得CD=AE,则可求得答案.
解答  (1)证明:连接AC,
(1)证明:连接AC,
∵CD⊥AB,AB是⊙O的直径,
∴$\widehat{AC}$=$\widehat{AD}$,
∵点C是$\widehat{AE}$的中点,
∴$\widehat{AC}$=$\widehat{CE}$,
∴$\widehat{CE}$=$\widehat{AD}$,
∴∠ACD=∠CAE,
∴AF=CF;
(2)∵在Rt△ACG中,tan∠BAE=$\frac{3}{4}$,
∴tan∠BAE=$\frac{FG}{AG}$=$\frac{3}{4}$,
∴设FG=3x,则AG=4x,
∴CF=AF=$\sqrt{A{G}^{2}+F{G}^{2}}$=5x,
∴CG=FG+CF=8x,
∵CD⊥AB,
∴CD=2CG=16x,
∵$\widehat{AC}$=$\widehat{AD}$=$\widehat{CE}$,
∴$\widehat{CD}$=$\widehat{AE}$,
∴CD=AE=8,
∴16x=8,
解得:x=$\frac{1}{2}$,
∴AF=5x=$\frac{5}{2}$.
点评 此题考查了圆周角定理、垂径定理、弧与弦、圆周角的关系等知识.注意利用方程思想求解是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果AD=5,AE=4,求⊙O的半径.
 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.(1)求证:DE是⊙O的切线;
(2)如果AD=5,AE=4,求⊙O的半径.
1.在下列方程中,一元二次方程是( )
| A. | x2-2xy+y2=0 | B. | x2-2x=3 | C. | x(x+3)=x2-1 | D. | x+$\frac{1}{x}$=0 |
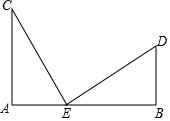 如图,已知AC⊥AB,DB⊥AB,AC=BE,CE=ED.求证:
如图,已知AC⊥AB,DB⊥AB,AC=BE,CE=ED.求证: