题目内容
已知x1,x2是方程x2+6x+3=0的两实数根,求①
+
,②x12+x22的值.
| x2 |
| x1 |
| x1 |
| x2 |
考点:根与系数的关系
专题:
分析:由x1,x2是方程x2+6x+3=0的两实数根,得出x1+x2=-6,x1x2=3;则①
+
=
;②x12+x22=(x1+x2)2-2x1x2;代入求得代数式的值.
| x2 |
| x1 |
| x1 |
| x2 |
| (x1+x2)2-2x1x2 |
| x1x2 |
解答:解:∵x1,x2是方程x2+6x+3=0的两实数根,
∴x1+x2=-6,x1x2=3;
①
+
=
=10;
②x12+x22=(x1+x2)2-2x1x2=30.
∴x1+x2=-6,x1x2=3;
①
| x2 |
| x1 |
| x1 |
| x2 |
| (x1+x2)2-2x1x2 |
| x1x2 |
②x12+x22=(x1+x2)2-2x1x2=30.
点评:此题考查根与系数的关系:x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的两个实数根,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
若|a-2|+|b+3|=0,则a+b的值是( )
| A、5 | B、1 | C、-1 | D、-5 |
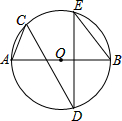 如图,AB为⊙O的直径,点C、D、E在圆上,AB⊥DE,∠ABE=50°,则∠ACD的度数是( )
如图,AB为⊙O的直径,点C、D、E在圆上,AB⊥DE,∠ABE=50°,则∠ACD的度数是( )| A、90° | B、50° |
| C、45° | D、30° |
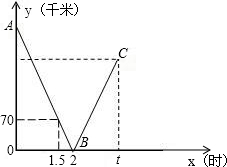 一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶40千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶40千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.