题目内容
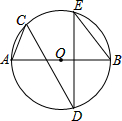 如图,AB为⊙O的直径,点C、D、E在圆上,AB⊥DE,∠ABE=50°,则∠ACD的度数是( )
如图,AB为⊙O的直径,点C、D、E在圆上,AB⊥DE,∠ABE=50°,则∠ACD的度数是( )| A、90° | B、50° |
| C、45° | D、30° |
考点:圆周角定理,垂径定理
专题:
分析:连接BD,先根据垂径定理得出BE=BD,故可得出∠ABD=∠ABE,再由圆周角定理即可得出结论.
解答: 解:∵连接BD,
解:∵连接BD,
∵AB为⊙O的直径,AB⊥DE,∠ABE=50°,
∴BE=BD,∠ABD=∠ABE=50°..
∵∠ACD与∠ABD是同弧所对的圆周角,
∴∠ACD=∠ABD=50°.
故选B.
 解:∵连接BD,
解:∵连接BD,∵AB为⊙O的直径,AB⊥DE,∠ABE=50°,
∴BE=BD,∠ABD=∠ABE=50°..
∵∠ACD与∠ABD是同弧所对的圆周角,
∴∠ACD=∠ABD=50°.
故选B.
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
如果|a|=3,那么a+1的值是( )
| A、4 | B、-2 |
| C、4或-2 | D、3或-3 |
已知点A(1,y1),B(2,y2),C(-3,y3)都在反比例函数y=
(k>0)的图象上,则y1,y2,y3的大小关系是( )
| k |
| x |
| A、y3<y1<y2 |
| B、y1<y2<y3 |
| C、y2<y1<y3 |
| D、y3<y2<y1 |
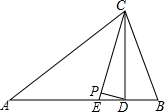 在△ABC中,∠A=38°,∠B=70°,CD⊥AB于点D,CE平分∠ACB,DP⊥CE于点P,求∠CDP的度数.
在△ABC中,∠A=38°,∠B=70°,CD⊥AB于点D,CE平分∠ACB,DP⊥CE于点P,求∠CDP的度数.