题目内容
15.两条直线y=ax+b与y=bx+a在同一直角坐标系中的图象位置可能是( )| A. |  | B. |  | C. |  | D. |  |
分析 对于各选项,先确定一条直线的位置得到a和b的符号,然后根据此符号判断另一条直线的位置是否符号要求.
解答 解:A、若经过第一、二、三象限的直线为y=ax+b,则a>0,b>0,所以直线y=bx+a经过第一、二、三象限,所以A选项错误;
B、若经过第一、三、四象限的直线为y=ax+b,则a>0,b<0,所以直线y=bx+a经过第一、二、四象限,所以B选项正确;
C、若经过第一、二、三象限的直线为y=ax+b,则a>0,b>0,所以直线y=bx+a经过第一、二、三象限,所以C选项错误;
D、若经过第一、三、四象限的直线为y=ax+b,则a>0,b<0,所以直线y=bx+a经过第一、二、四象限,所以D选项错误;
故选B.
点评 本题考查了一次函数图象与系数的关系,一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.在x=0,-$\frac{5}{2}$,3,$\frac{5}{3}$中,满足不等式组$\left\{\begin{array}{l}{\frac{x}{2}<1}\\{2(x+1)>-2}\end{array}\right.$的x值是( )
| A. | 0和-$\frac{5}{2}$ | B. | -$\frac{5}{2}$和$\frac{5}{3}$ | C. | 0和3 | D. | 0和$\frac{5}{3}$ |
 已知如图所示的Rt△ABC中,两直角边a、b满足a-b=1,斜边c=5,求△ABC的面积和周长.
已知如图所示的Rt△ABC中,两直角边a、b满足a-b=1,斜边c=5,求△ABC的面积和周长.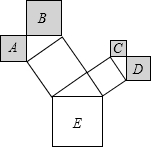 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,4,1,2,则最大的正方形E的面积是9.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,4,1,2,则最大的正方形E的面积是9.