题目内容
13．已知关于x的一元二次方程x2+ax+b=0有一个非零根b，则a+b的值为（ ）| A． | 1 | B． | -1 | C． | 0 | D． | 一2 |
分析 根据一元二次方程的解的定义，把x=b代入x2+ax+b=0得b2+ab+b=0，然后把等式两边除以b即可．
解答 解：把x=b代入x2+ax+b=0得b2+ab+b=0，
而b≠0，
所以b+a+1=0，
所以a+b=-1．
故选B．
点评 本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．
练习册系列答案
中考利剑中考试卷汇编系列答案
相关题目
7．
小亮早晨从家骑车到学校，先上坡后下坡，行程情况如图所示．若返回时上坡、下坡的速度仍保持不变，那么小明从学校骑车回家用的时间是（ ）
小亮早晨从家骑车到学校，先上坡后下坡，行程情况如图所示．若返回时上坡、下坡的速度仍保持不变，那么小明从学校骑车回家用的时间是（ ）| A． | 37.2分钟 | B． | 48分钟 | C． | 33分钟 | D． | 30分钟 |
4．与2和为0的数是（ ）
| A． | -2 | B． | 2 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
1．圆锥的主视图是边长为4cm的等边三角形，则该圆锥俯视图的面积是（ ）
| A． | 4π cm2 | B． | 8π cm2 | C． | 12π cm2 | D． | 16π cm2 |
8．下列命题中，正确的个数是（ ）
①若三条线段的比为1：1：$\sqrt{2}$，则它们组成一个等腰直角三角形；②两条对角线相等的平行四边形是矩形；③对角线互相垂直的四边形是菱形；④一条直线与矩形的一组对边相交，可分矩形为两个面积相等的梯形．
①若三条线段的比为1：1：$\sqrt{2}$，则它们组成一个等腰直角三角形；②两条对角线相等的平行四边形是矩形；③对角线互相垂直的四边形是菱形；④一条直线与矩形的一组对边相交，可分矩形为两个面积相等的梯形．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
18．已知关于x的一元二次方程x2-2x+k=0有两个不相等的实数根，则k的值可以是（ ）
| A． | -2 | B． | 1 | C． | 2 | D． | 3 |
4．一组数据6，6，6，6，6，6，6的方差为m，若增加一个数0，则新数据的方差比原数据的方差是（ ）
| A． | 变大 | B． | 减小 | C． | 不变 | D． | 无法确定 |
1．有下列四个论断：①-$\frac{1}{3}$是有理数；②$\frac{\sqrt{2}}{2}$是分数；③1.232232223…是无理数；④π是无理数，其中正确的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
2．如图，若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状，并使其最小内角为30°，则下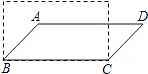
面说法正确的是（ ）
面说法正确的是（ ）| A． | 面积变为原来的一半，周长不变 | B． | 周长变为原来的一半，面积不变 | ||
| C． | 周长和面积都变为原来的一半 | D． | 周长和面积都不变 |