题目内容
20.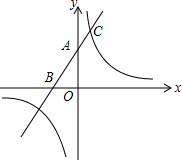 如图,在平面直角坐标系中,直线l:y1=2x+4,与y轴交于点A,与x轴交于点B,反比例函数y2=$\frac{k}{x}$与直线l交于点C,且AB=2AC.
如图,在平面直角坐标系中,直线l:y1=2x+4,与y轴交于点A,与x轴交于点B,反比例函数y2=$\frac{k}{x}$与直线l交于点C,且AB=2AC.(1)求反比例函数的解析式;
(2)根据函数图象,直接写出0<y1<y2的x的取值范围.
分析 由OB∥CH得△ABO∽△ACH得$\frac{OA}{AH}=\frac{OB}{CH}=\frac{AB}{AC}=2$,由此可以求出点P坐标.
解答 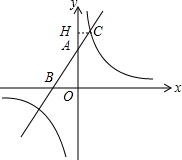 解:(1)如图,过点C作CH⊥y轴,垂足为H.
解:(1)如图,过点C作CH⊥y轴,垂足为H.
把x=0代入y1=2x+4得,y=4,
把y=0,代入y1=2x+4得,x=-2,
∴A点坐标为(0,4),B点坐标为(-2,0),
∴OB=2,OA=4,
∵OB∥CH,
∴△ABO∽△ACH
∴$\frac{OA}{AH}=\frac{OB}{CH}=\frac{AB}{AC}=2$,
即$\frac{4}{AH}=\frac{2}{CH}=2$,
解得AH=2,CH=1,
∴OH=6
∴点C坐标为(1,6)
把点C作标代入反比例函数解析式,得k=6
∴反比例函数的解析式为y=$\frac{6}{x}$.
(2)∵点C坐标(1,6),
∴由图象可知,0<y1<y2解析时,0<x<1.
点评 本题考查一次函数与反比例函数的交点问题、相似三角形的判定和性质、待定系数法确定反比例函数的解析式,解题的关键是发现相似三角形解决问题,属于中考常考题型.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
10.若菱形的两条对角线的长分别为6,8.则此菱形的周长是( )
| A. | 14 | B. | 20 | C. | 28 | D. | 40 |
8.已知⊙O1与⊙O2外离,⊙O1的半径是5,圆心距O1O2=7,那么⊙O2的半径可以是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
15.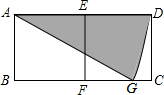 如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
 如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
9. 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定点投篮进球数进行整理,作出如下统计图表.
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表:
(1)选择长跑训练的人数占全班人数的百分比是10%,该班共有同学40人.
(2)求训练后篮球定点投篮人均进球数为多少个?
(3)根据测试资料,参加篮球定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定点投篮进球数进行整理,作出如下统计图表.
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定点投篮进球数进行整理,作出如下统计图表.训练后篮球定点投篮测试进球统计表:
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(2)求训练后篮球定点投篮人均进球数为多少个?
(3)根据测试资料,参加篮球定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;过点B的直线DE分别交l1、l3于点D、E.若AB=2,BC=4,BD=1.5,则线段BE的长为3.
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;过点B的直线DE分别交l1、l3于点D、E.若AB=2,BC=4,BD=1.5,则线段BE的长为3.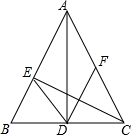 如图,已知等腰△ABC中,AB=AC,AD⊥BC,CE⊥AB,垂足分别为D、E.
如图,已知等腰△ABC中,AB=AC,AD⊥BC,CE⊥AB,垂足分别为D、E.