题目内容
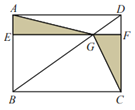
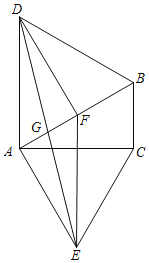
【题目】如图,正方形 ABCD 中,AB=4,点 E为边AD上一动点,连接 CE,以 CE为边,作正方形CEFG(点D、F在CE所在直线的同侧),H为CD中点,连接 FH.
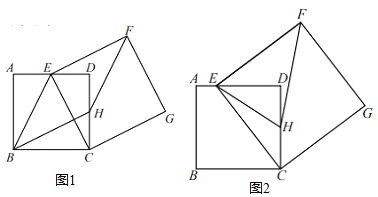
(1)如图 1,连接BE,BH,若四边形 BEFH 为平行四边形,求四边形 BEFH 的周长;
(2)如图 2,连接 EH,若 AE=1,求△EHF 的面积;
(3)直接写出点E在运动过程中,HF的最小值.
【答案】(1)8![]() ;(2)
;(2)![]() ;(3)3
;(3)3![]() .
.
【解析】
(1)由平行四边形的性质和正方形的性质可得EC=EF=BH,BC=DC,可证Rt△BHC≌Rt△CED,可得CH=DE,由“SAS”可证BE=EC,可得BE=EF=HF=BH=EC,由勾股定理可求BH的长,即可求四边形BEFH的周长;
(2)连接DF,过点F作FM⊥AD,交AD延长线于点M,由“AAS”可证△EFM≌△CED,可得CD=EM=4,DE=FM=3,由三角形面积公式可求解;
(3)过点F作FN⊥CD的延长线于点N,设AE=x=DM,则DE=4-x=FM,NH=4-x+2=6-x,由勾股定理可求HF的长,由二次函数的性质可求HF的最小值.
解:(1)∵四边形BEFH为平行四边形
∴BE=HF,BH=EF
∵四边形EFGC,四边形ABCD都是正方形
∴EF=EC,BC=CD=4=AD
∴BH=EC,且BC=CD
∴Rt△BHC≌Rt△CED(HL)
∴CH=DE
∵H为CD中点,
∴CH=2=DE
∴AE=AD-DE=2=DE,且AB=CD,∠BAD=∠ADC=90°
∴Rt△ABE≌Rt△DCE(SAS)
∴BE=EC
∴BE=EF=HF=BH=EC
∵CH=2,BC=4
∴BH=![]() =
=![]() =2
=2![]()
∴四边形BEFH的周长=BE+BH+EF+FH=8![]() ;
;
(2)如图2,连接DF,过点F作FM⊥AD,交AD延长线于点M,
∵AE=1,
∴DE=3
∵∠FEM+∠CEM=90°,∠CEM+∠ECD=90°
∴∠FEM=∠ECD,且CE=EF,∠EDC=∠EMF=90°
∴△EFM≌△CED(AAS)
∴CD=EM=4,DE=FM=3,
∴DM=1,
∴S△EFH=S△EFD+S△EDH+S△DHF=![]() ×3×3+
×3×3+![]() ×3×2+
×3×2+![]() ×2×1=
×2×1=![]() ;
;
(3)如图3,过点F作FN⊥CD的延长线于点N,
由(2)可知:△EFM≌△CED
∴CD=EM,DE=FM,
∴CD=AD=EM,
∴AE=DM,
设AE=x=DM,则DE=4-x=FM,
∵FN⊥CD,FM⊥AD,ND⊥AD
∴四边形FNDM是矩形
∴FN=DM=x,FM=DN=4-x
∴NH=4-x+2=6-x
在Rt△NFH中,HF=![]() =
=![]() =
=![]()
∴当x=3时,HF有最小值=![]() =3
=3![]() .
.
故答案为:(1)8![]() ;(2)
;(2)![]() ;(3)3
;(3)3![]() .
.

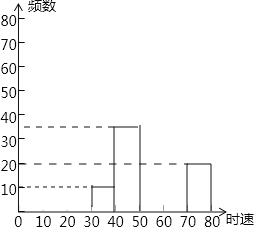
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30﹣40含起点值30,不含终点值40),得到其频数及频率如表:
数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | c |
50﹣60 | a | 0.39 |
60﹣70 | b | d |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
(1)表中a、b、c、d分别为:a= ; b= ; c= ; d=
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?