题目内容
7.已知y与x2成反比例,且当x=-2时,y=2,那么当x=4时,y=( )| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -4 |
分析 根据y与x2成反比例,可以列出y与x2函数关系式,由x=-2时,y=2,可以求得函数关系式中的k的值,再将x=4代入关系式,即可求得y的值,本题得以解决.
解答 解:∵y与x2成反比例,
∴设y=$\frac{k}{{x}^{2}}$,
∵x=-2时,y=2,
∴2=$\frac{k}{(-2)^{2}}$,得k=8,
将x=4代入y=$\frac{8}{{x}^{2}}$,得y=$\frac{8}{{4}^{2}}$=$\frac{1}{2}$,
故选C.
点评 本题考查反比例函数的定义,解题的关键是明确题意,求出函数关系式,当x确定时,根据关系式可以求相应的y的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.某学习小组9名学生参加“数学竞赛”,他们的得分情况如表:
那么这9名学生所得分数的众数和中位数分别是( )
| 人数(人) | 1 | 3 | 4 | 1 |
| 分数(分) | 80 | 85 | 90 | 95 |
| A. | 90,90 | B. | 90,85 | C. | 90,87.5 | D. | 85,85 |
15.已知α、β均为锐角,且满足|sinα-$\frac{1}{2}$|+$\sqrt{(tanβ-1)^{2}}$=0,则α+β=( )
| A. | 60° | B. | 75° | C. | 90° | D. | 105° |
2.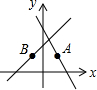 如图,在平面直角坐标系中,点A(1,m)在直线y=-2x+3上,点A关于y轴的对称点恰好落在直线y=kx+2上,则k的值为( )
如图,在平面直角坐标系中,点A(1,m)在直线y=-2x+3上,点A关于y轴的对称点恰好落在直线y=kx+2上,则k的值为( )
 如图,在平面直角坐标系中,点A(1,m)在直线y=-2x+3上,点A关于y轴的对称点恰好落在直线y=kx+2上,则k的值为( )
如图,在平面直角坐标系中,点A(1,m)在直线y=-2x+3上,点A关于y轴的对称点恰好落在直线y=kx+2上,则k的值为( )| A. | -2 | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
16.若P在第二象限,且到x轴的距离为3,到y轴的距离为6,则点P的坐标为( )
| A. | (3,6) | B. | (-3,6) | C. | (-6,3) | D. | (6,3) |
17.汽车向南行驶10千米记作10千米,那么汽车向北行驶10千米记作( )
| A. | 0千米 | B. | -10千米 | C. | -20千米 | D. | 10千米 |
 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).