题目内容
9.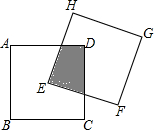 如图,两个边长相等的正方形ABCD和EFGH,将正方形EFGH的顶点E固定在正方形ABCD的对称中心,正方形EFGH绕点E顺时针方向旋转;设旋转的角度为θ(0°≤θ≤360°),两个正方形重叠部分的面积为S,则S与θ的函数关系的大致图象是( )
如图,两个边长相等的正方形ABCD和EFGH,将正方形EFGH的顶点E固定在正方形ABCD的对称中心,正方形EFGH绕点E顺时针方向旋转;设旋转的角度为θ(0°≤θ≤360°),两个正方形重叠部分的面积为S,则S与θ的函数关系的大致图象是( )| A. | 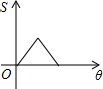 | B. | 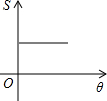 | C. | 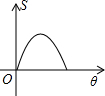 | D. | 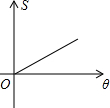 |
分析 过点E作EM⊥CD于点M,EN⊥AD于点N,则可证明△ENK≌△EML,从而得出重叠部分的面积不变,继而可得出函数关系图象
解答 解:如右图,过点E作EM⊥CD于点M,EN⊥AD于点N,
∵点E是正方形的对称中心,
∴EN=EM,
由旋转的性质可得∠NEK=∠MEL,
在Rt△ENK和Rt△EML中,
$\left\{\begin{array}{l}{∠NEK=∠EML}\\{EN=EM}\\{∠ENK=∠EML}\end{array}\right.$,
故可得△ENK≌△EML,即阴影部分的面积始终等于正方形面积的$\frac{1}{4}$.
故选:B.
点评 此题考查了动点问题的函数图象,证明△ENK≌△EML,得出阴影部分的面积始终等于正方形面积的$\frac{1}{4}$是解答本题的关键.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
19.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | C. | $\sqrt{2}$$•\sqrt{3}$=$\sqrt{6}$ | D. | $\sqrt{8}$$÷\sqrt{2}$=4 |
 如图,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为135°.
如图,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为135°.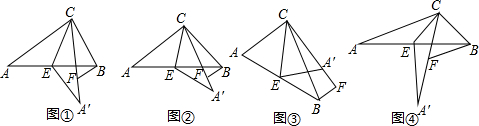
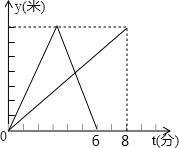 小华和爷爷在一环形跑道上匀速跑步,两人在同一起点顺时针出发,两人离起点较近的环形距离y与时间t之间关系如图所示,出发后小华第一次与爷爷相遇的时间为9.6分.
小华和爷爷在一环形跑道上匀速跑步,两人在同一起点顺时针出发,两人离起点较近的环形距离y与时间t之间关系如图所示,出发后小华第一次与爷爷相遇的时间为9.6分.