题目内容
13.为了迎接“清明”小长假的购物高峰,某运动品牌服装店准备购进甲、乙两种服装,已知每件甲服装进价比每件乙服装进价多20元,售价在进价的基础上加价50%,通过初步预算,若以4800元购进的甲服装比以4200元购进乙服装的件数少10件.(1)求甲、乙两种服装的销售单价;
(2)现老板计划购进两种服装共100件,其中甲种服装不少于65件,若购进这100件服装的费用不超过7500元,则甲种服装最多购进多少件?
(3)在(2)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
分析 (1)设甲服装进价为x元/件,则乙服装进价为(x-20)元/件,根据“以4800元购进的甲服装比以4200元购进乙服装的件数少10件”列分式方程求解即可;
(2)设甲种服装购进m件,则乙种服装购进(100-m)件,然后根据购进这100件服装的费用不得超过7500元,列出不等式解答即可;
(3)首先求出总利润W的表达式,然后针对a的不同取值范围进行讨论,分别确定其进货方案.
解答 解:(1)设甲服装进价为x元/件,则乙服装进价为(x-20)元/件,
根据题意,得:$\frac{4800}{x}$=$\frac{4200}{x-20}$-10,
整理,得:x2+40x-9600=0,
解得:x1=-120(舍),x2=80,
经检验x=80是原分式方程的解,
∴甲服装的销售单件为80×(1+50%)=120元/件,
乙服装的销售单价为(80-20)×(1+50%)=90元/件;
答:甲服装的销售单件为120元/件,乙服装的销售单价为90元/件.
(2)设购进甲种服装m件,则可购进乙种服装(100-m)件,
根据题意,得:$\left\{\begin{array}{l}{m≥65}\\{80m+60(100-m)≤7500}\end{array}\right.$,
解得:65≤m≤75,
答:甲种服装最多购进75件.
(3)设总利润为W元,
W=(120-80-a)x+(90-60)(100-x)
即w=(10-a)x+3000.
①当0<a<10时,10-a>0,W随x增大而增大,
∴当x=75时,W有最大值,即此时购进甲种服装75件,乙种服装25件;
②当a=10时,所以按哪种方案进货都可以;
③当10<a<20时,10-a<0,W随x增大而减小.
当x=65时,W有最大值,即此时购进甲种服装65件,乙种服装35件.
点评 本题考查了分式方程的应用、不等式组的应用、以及一次函数的性质,正确利用x表示出利润并根据一次项系数分类讨论是关键.

 阅读快车系列答案
阅读快车系列答案 某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):
某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):88,85,90,99,86,68,94,98,78,97
96,93,89,94,89,85,80,95,89,77
请根据上述数据,解决下列问题:
(1)补全下面考生素描成绩的表格(每组数据含最小值不含最大值)和频数分布直方图;
| 分组 | 人数(频数) |
| 60-70 | 1 |
| 70-80 | 2 |
| 80-90 | 9 |
| 90-100 | 8 |
| 合计 | 20 |
| 项目 成绩 | 素描 | 色彩 | 速写 |
| 甲 | 98 | 93 | 95 |
| 乙 | 95 | 95 | 100 |
| A. | $\root{3}{1}=±1$ | B. | $\sqrt{{{({-3})}^2}}=3$ | C. | $-\sqrt{0.81}=0.9$ | D. | $\sqrt{9}=±3$ |
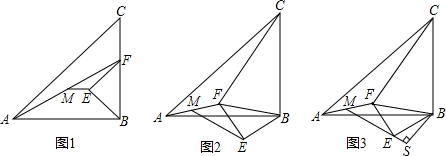
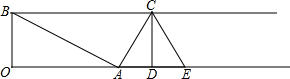 如图,射线BC∥射线OA,BO⊥OA,且OB=2,OA=4,过点A作AC⊥AB交射线BC于C,过点C作CD⊥射线OA交射线OA于D,A,E关于直线CD对称,将△CDE沿射线BC向左向右平移得到△C′D′E′.再将以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形拼成不重叠无缝隙的图形恰好是三角形,请写出所有符合上述条件的BC′的长6或1.
如图,射线BC∥射线OA,BO⊥OA,且OB=2,OA=4,过点A作AC⊥AB交射线BC于C,过点C作CD⊥射线OA交射线OA于D,A,E关于直线CD对称,将△CDE沿射线BC向左向右平移得到△C′D′E′.再将以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形拼成不重叠无缝隙的图形恰好是三角形,请写出所有符合上述条件的BC′的长6或1.