题目内容
6.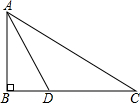 如图,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果保留根号)
如图,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果保留根号)
分析 根据题意得∠C=30°,∠ADB=60°,从而得到∠DAC=30°,进而判定AD=CD,得到CD=20米,在Rt△ADB中利用sin∠ADB求得AB的长即可.
解答 解:∵∠C=30°,∠ADB=60°,
∴∠DAC=30°,
∴AD=CD,
∵CD=20米,
∴AD=20米,
在Rt△ADB中,
$\frac{AB}{AD}$=sin∠ADB,
∴AB=AD×sin60°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$米.
点评 此题主要考查了解直角三角形的应用,解题的关键是从题目中整理出直角三角形并正确的利用边角关系求解.

练习册系列答案
相关题目
1.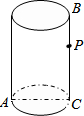 如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=$\frac{2}{3}$BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=$\frac{2}{3}$BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
 如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=$\frac{2}{3}$BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=$\frac{2}{3}$BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )| A. | (4+$\frac{6}{π}$)cm | B. | 5cm | C. | 2$\sqrt{13}$cm | D. | 7cm |
11.下列计算结果正确的是( )
| A. | 2a3+a3=3a6 | B. | (-a)2•a3=-a6 | C. | (-$\frac{1}{2}$)-2=4 | D. | (-2)0=-1 |
 如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为( )
如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为( ) 中国“蛟龙”号深潜器目前最大测潜极限为7062.68米,某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
中国“蛟龙”号深潜器目前最大测潜极限为7062.68米,某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°. 我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA 由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是7个.
由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是7个.