题目内容
3.观察下列各式的特点:$\sqrt{1}$=1,$\sqrt{1+3}$=2,$\sqrt{1+3+5}$=3,$\sqrt{1+3+5+7}$=4,…
计算:$\frac{1}{\sqrt{1}×\sqrt{1+3}}$+$\frac{1}{\sqrt{1+3}×\sqrt{1+3+5}}$+…+$\frac{1}{\sqrt{1+3+…+2015}×\sqrt{1+3+…+2017}}$=$\frac{1008}{1009}$.
分析 先利用题中的规律化简二次根式得到原式=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{1008×1009}$,然后利用$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$把每个分数分成两个分数的差,再进行分数的运算即可.
解答 解:原式=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{1008×1009}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{1008}$-$\frac{1}{1009}$
=1-$\frac{1}{1009}$
=$\frac{1008}{1009}$.
故答案为$\frac{1008}{1009}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
相关题目
 如图,BD,CE相交于点A,且AB=AD AC=AE.求证:BC∥DE.
如图,BD,CE相交于点A,且AB=AD AC=AE.求证:BC∥DE. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,则关于x的一元一次方程ax2+bx+c=2(a≠0)的解为0或2.
已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,则关于x的一元一次方程ax2+bx+c=2(a≠0)的解为0或2.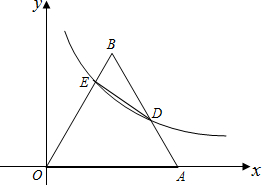 如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),反比例函数y=$\frac{k}{x}$(x>0,k≠0)的图象经过AB的中点D,交OB于E.
如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),反比例函数y=$\frac{k}{x}$(x>0,k≠0)的图象经过AB的中点D,交OB于E.