题目内容
 如图,已知⊙O的半径为2,弦BC的长为2,点A为弦BC所对优弧上任意一点(B,C两点除外).
如图,已知⊙O的半径为2,弦BC的长为2,点A为弦BC所对优弧上任意一点(B,C两点除外).(1)求∠BAC的度数;
(2)求△ABC面积的最大值.
考点:圆周角定理,三角形的面积,等腰三角形的判定与性质
专题:计算题
分析:(1)连结OB、OC,如图,证明△OBC为等边三角形得到∠BOC=60°,然后根据圆周角定理求解;
(2)作OH⊥BC于H,交⊙O于D,连结DB、DC,则点D为优弧BC的中点,根据等边三角形的性质得OH=
BC=
,则可计算出S△BDC=2+
,由于点A为弦BC所对优弧的中点时,点A到BC的距离最大,此时△ABC面积的最大,所以△ABC面积的最大值为2+
.
(2)作OH⊥BC于H,交⊙O于D,连结DB、DC,则点D为优弧BC的中点,根据等边三角形的性质得OH=
| ||
| 2 |
| 3 |
| 3 |
| 3 |
解答:解:(1)连结OB、OC,如图,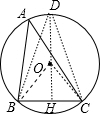
∵OB=OC=2,BC=2,
∴OB=OC=BC,
∴△OBC为等边三角形,
∴∠BOC=60°,
∴∠BAC=
∠BOC=30°;
(2)作OH⊥BC于H,交⊙O于D,连结DB、DC,则点D为优弧BC的中点,
∵△OBC为等边三角形,
∴OH=
BC=
,
∴S△BDC=
×2×(2+
)=2+
,
∵点A为弦BC所对优弧的中点时,点A到BC的距离最大,此时△ABC面积的最大,
∴△ABC面积的最大值为2+
.

∵OB=OC=2,BC=2,
∴OB=OC=BC,
∴△OBC为等边三角形,
∴∠BOC=60°,
∴∠BAC=
| 1 |
| 2 |
(2)作OH⊥BC于H,交⊙O于D,连结DB、DC,则点D为优弧BC的中点,
∵△OBC为等边三角形,
∴OH=
| ||
| 2 |
| 3 |
∴S△BDC=
| 1 |
| 2 |
| 3 |
| 3 |
∵点A为弦BC所对优弧的中点时,点A到BC的距离最大,此时△ABC面积的最大,
∴△ABC面积的最大值为2+
| 3 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等边三角形的判定与性质.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
若m与3互为相反数,则|m+3|等于( )
A、
| ||
B、
| ||
| C、0 | ||
| D、3 |
 某公司举办汇演,安排了一个“抽奖“环节;在一个不透明的盒子里,放入4个除颜色外均相等的彩球,其中红球2个,黄球1个,篮球1个,每人一次从盒子中任意摸出两个球.
某公司举办汇演,安排了一个“抽奖“环节;在一个不透明的盒子里,放入4个除颜色外均相等的彩球,其中红球2个,黄球1个,篮球1个,每人一次从盒子中任意摸出两个球.

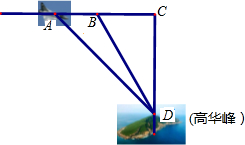 钓鱼岛自古以来就是我国神圣领土,2012年9月21日,国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并开始对钓鱼岛进行常态化立体巡航.如图,再一次巡航过程中,混巡航飞机飞行高度为4148米,在点A测得高华峰顶D点俯角为45°,飞机保持方向不变,前进1600米到达B点后测得D点俯角为60°,请据此钓鱼岛的最高峰海拔高度DE约为多少米.(结果保留整数,参考数值:
钓鱼岛自古以来就是我国神圣领土,2012年9月21日,国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并开始对钓鱼岛进行常态化立体巡航.如图,再一次巡航过程中,混巡航飞机飞行高度为4148米,在点A测得高华峰顶D点俯角为45°,飞机保持方向不变,前进1600米到达B点后测得D点俯角为60°,请据此钓鱼岛的最高峰海拔高度DE约为多少米.(结果保留整数,参考数值: 尺规作图:(不写作法,保留作图痕迹)如图,已知∠MON,求作射线OP,使∠MOP=∠NOP.
尺规作图:(不写作法,保留作图痕迹)如图,已知∠MON,求作射线OP,使∠MOP=∠NOP.