题目内容
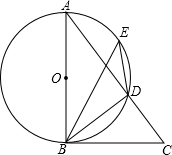如图，AB是⊙O的直径，点E是 |
| AD |
（1）求证：BC是⊙O的切线；
（2）已知AD=3，CD=2，求BC的长．
考点：切线的判定,相似三角形的判定与性质
专题：证明题
分析：（1）AB是⊙O的直径，得∠ADB=90°，从而得出∠BAD=∠DBC，即∠ABC=90°，即可证明BC是⊙O的切线；
（2）可证明△ABC∽△BDC，则
=
，即可得出BC=
．
（2）可证明△ABC∽△BDC，则
| BC |
| CA |
| CD |
| BC |
| 10 |
解答：（1）证明：∵AB是⊙O的切直径，
∴∠ADB=90°，
又∵∠BAD=∠BED，∠BED=∠DBC，
∴∠BAD=∠DBC，
∴∠BAD+∠ABD=∠DBC+∠ABD=90°，
∴∠ABC=90°，
∴BC是⊙O的切线；
（2）解：∵∠BAD=∠DBC，∠C=∠C，
∴△ABC∽△BDC，
∴
=
，即BC2=AC•CD=（AD+CD）•CD=10，
∴BC=
．
∴∠ADB=90°，
又∵∠BAD=∠BED，∠BED=∠DBC，
∴∠BAD=∠DBC，
∴∠BAD+∠ABD=∠DBC+∠ABD=90°，
∴∠ABC=90°，
∴BC是⊙O的切线；
（2）解：∵∠BAD=∠DBC，∠C=∠C，
∴△ABC∽△BDC，
∴
| BC |
| CA |
| CD |
| BC |
∴BC=
| 10 |
点评：本题考查了切线的判定以及相似三角形的判定和性质，是重点知识要熟练掌握．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
在实数：3.14159，
，1.010010001…，4.
，π，
，
中，无理数有（ ）
| 3 | 64 |
| •• |
| 21 |
| 3 |
| 22 |
| 7 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如图，在△ABC和△ABD中，AC与BD相交于点E，AD=BC，∠DAB=∠CBA，求证：AC=BD．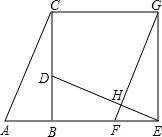
如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DE、FG相交于点H．