题目内容
11.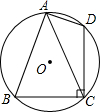 如图,△ABC内接于⊙O,弦DC⊥BC,已知⊙O的半径为5cm,弦BC长为6cm,则tan∠BAC=$\frac{3}{4}$.
如图,△ABC内接于⊙O,弦DC⊥BC,已知⊙O的半径为5cm,弦BC长为6cm,则tan∠BAC=$\frac{3}{4}$.
分析 首先连接BD,由弦DC⊥BC,易得BD是直径,然后由勾股定理求得CD的长,又由圆周角定理,求得∠BDC=∠BAC,继而求得答案.
解答 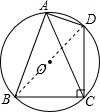 解:连接BD,
解:连接BD,
∵弦DC⊥BC,
∴∠BCD=90°,
∴BD是直径,
∵⊙O的半径为5cm,弦BC长为6cm,
∴BD=10cm,
∴CD=$\sqrt{B{D}^{2}-B{C}^{2}}$=8cm,
∴tan∠BAC=tan∠BDC=$\frac{BC}{CD}$=$\frac{6}{8}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 此题考查了圆周角定理、勾股定理以及三角函数的定义.注意准确作出辅助线是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列调查适合作抽样调查的是( )
| A. | 了解巫溪网“今日巫溪”栏目的阅览率 | |
| B. | 了解某甲型H1N1确诊病人同机乘客的健康状况 | |
| C. | 了解某班每个学生家庭电脑的数量 | |
| D. | 对“歼20”隐形战斗机零部件的检查 |
6.下列实数中,是负数的是( )
| A. | -$\sqrt{2}$ | B. | 2.5 | C. | 0 | D. | $\frac{5}{7}$ |
16.用配方法解方程x2+4x-5=0,下列配方正确的是( )
| A. | (x+2)2=1 | B. | (x+2)2=5 | C. | (x+2)2=9 | D. | (x+4)2=9 |
3.函数$y=\frac{{\sqrt{2-x}}}{x-3}$的自变量x的取值范围是( )
| A. | x≤2 | B. | x≥2且x≠3 | C. | x≥2 | D. | x≤2且x≠3 |
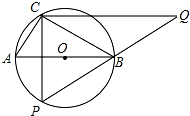 如图,在⊙O上有定点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为5,tan∠ABC=$\frac{3}{4}$,则CQ的最大值为$\frac{20}{3}$.
如图,在⊙O上有定点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为5,tan∠ABC=$\frac{3}{4}$,则CQ的最大值为$\frac{20}{3}$.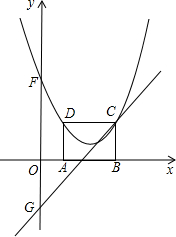 如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=2,直线y=x-2经过点C,交y轴于点G.
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=2,直线y=x-2经过点C,交y轴于点G.