题目内容
2.在直径为8cm的圆外有一点P,点P到圆上的点的最短距离为4cm,则过点P的圆的切线长为( )| A. | 4cm | B. | $4\sqrt{2}$cm | C. | $4\sqrt{3}$cm | D. | 6cm |
分析 作射线PO,得到点P到圆上的点的最短距离,根据切割线定理,列出算式,求出切线长.
解答 解:如图作射线PO,交⊙O与A、B两点,则PA为点P到圆上的点的最短距离为4cm,
AB=8cm,PC为⊙O的切线,
根据切割线定理,
PC2=PA•PB=4×(4+8)=48,
PC=4$\sqrt{3}$cm.
故选:C.
点评 本题考查的是切线的性质和点与圆的位置关系,理解圆外一点到圆上的点的最短距离和最长距离是解题的关键,解答时,注意切线的有关定理的灵活运用.

练习册系列答案
相关题目
17.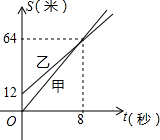 甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )
甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )
 甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )
甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )| A. | 2.5米 | B. | 2米 | C. | 1.5米 | D. | 1米 |
3.若∠α与∠β是内错角,且∠α=50°时,则∠β的度数为( )
| A. | 50° | B. | 130° | C. | 50°或130° | D. | 无法确定 |
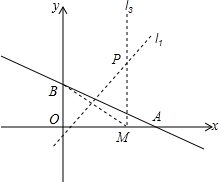 如图:直线y=kx+3与x轴、y轴分别交于A、B两点,tan∠OAB=$\frac{3}{4}$,点M是x轴上的一个动点.连接BM,作线段BN的垂直平分线l1,过点M作x轴垂线l2 记l1与l2的交点为P.
如图:直线y=kx+3与x轴、y轴分别交于A、B两点,tan∠OAB=$\frac{3}{4}$,点M是x轴上的一个动点.连接BM,作线段BN的垂直平分线l1,过点M作x轴垂线l2 记l1与l2的交点为P.