题目内容
19.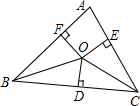 如图,O是△ABC内一点,且O到△ABC三边AB、BC、CA的距离OF=OE=OD,若∠BAC=70°,则∠BOC=125°.
如图,O是△ABC内一点,且O到△ABC三边AB、BC、CA的距离OF=OE=OD,若∠BAC=70°,则∠BOC=125°.
分析 根据到角的两边距离相等的点在角的平分线上判断出点O是三角形三条角平分线的交点,再根据三角形的内角和定理求出∠ABC+∠ACB,然后求出∠OBC+∠OCB,再利用三角形的内角和定理列式计算即可得解.
解答 解:∵O到三边AB、BC、CA的距离OF=OD=OE,
∴点O是三角形三条角平分线的交点,
∵∠BAC=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×110°=55°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
故答案为:125°.
点评 本题考查了角平分线的性质,三角形的内角和定理,熟练掌握角平分线的性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.若(b-1)2+a2=0,则下列方程中是关于x的一元二次方程的是( )
| A. | ax2+5x-b=0 | B. | (b2-1)x2+(a+3)x-5=0 | C. | (a-1)x2+(b-1)x-7=0 | D. | (b-1)x2+ax-1=0 |
8. 反比例函数y=$\frac{k}{x}$的图象如图所示,则k的值可能是( )
反比例函数y=$\frac{k}{x}$的图象如图所示,则k的值可能是( )
 反比例函数y=$\frac{k}{x}$的图象如图所示,则k的值可能是( )
反比例函数y=$\frac{k}{x}$的图象如图所示,则k的值可能是( )| A. | 1 | B. | -4 | C. | 0 | D. | $\sqrt{3}$ |
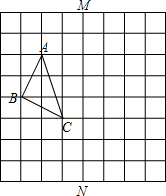 如图,在正方形网格中有一个△ABC,顶点A,B,C在格点上
如图,在正方形网格中有一个△ABC,顶点A,B,C在格点上 如图,△ABC中,AB的垂直平分线交AC与点M.若CM=4cm,BC=5cm,AM=6cm,则△MBC的周长=15cm.
如图,△ABC中,AB的垂直平分线交AC与点M.若CM=4cm,BC=5cm,AM=6cm,则△MBC的周长=15cm.