Question

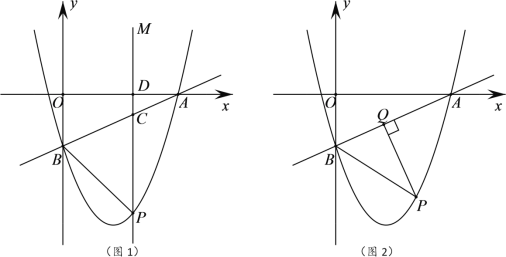
【题目】如图1，在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）的图象与x轴交于A，B两点，与y轴交于点C（0，3），且抛物线的顶点坐标为（1，4）．

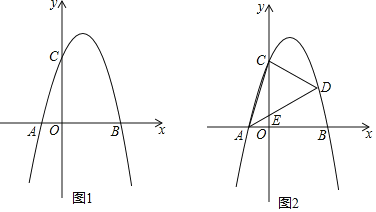
（1）求抛物线的解析式；

（2）如图2，点D是第一象限抛物线上的一点，AD交y轴于点E，设点D的横坐标为m，设△CDE的面积为S，求S与m的函数关系式（不必写出自变量的取值范围）；

（3）在（2）的条件下，连接AC，是否存在这样的点D，使得∠DAB＝2∠ACO，若存在，求点D的坐标及相应的S的值，若不存在，请说明理由．

Answer 1

【答案】(1)抛物线的表达式为：y=﹣x2+2x+3；(2)S=m2；(3)存在，点D的坐标为(，)，相应的S的值为

【解析】

(1)设抛物线的表达式为：()2+4，将C的坐标代入，即可求解；

(2)S=S△CED =CExD=m2；

(3)求出sin∠ACM==sin∠DAB，则tan∠DAB=，得到直线AE的表达式，即可求解．

(1)设抛物线的表达式为：()2()2+4，

将点C的坐标代入得：()2+4=3，

解得：，

∴抛物线的表达式为：()2+4①；

(2)点D的横坐标为m，则点D的坐标为(m，﹣m2+2m+3)，

设直线AD的表达式为：，

则，解得，

∴直线AD的表达式为：，

∴点E的坐标为(，)，则，

则S=S△CED =CExD=mm=m2；

(3)存在，理由：

令，则()2+4=0，

解得：，

∴点A的坐标为(，)，点B的坐标为(，)，

在OB上截取OM=OA=1，故点M(1，0)，

则∠MCO=∠ACO，

∵∠DAB=2∠ACO，

∴∠ACM=∠DAB，

在△ACM中，设CM边上的高为h，

AC=MC==，

则S△AMC=，即2×3=h，

解得：h=，

在△ACM中，sin∠ACM====sin∠DAB，

则tan∠DAB=，

在Rt△AOE中，OA=1，tan∠DAB=，

则OE=，故点E(0，)，

设直线AE的表达式为：，

则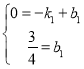，解得：，

∴直线AE的表达式为：y=x+②，

联立①②并解得：=或﹣1(舍去﹣1)，

∴点D的坐标为(，)，

由(2)知，S=m2 ==，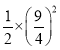

∴点D的坐标为(，)，相应的S的值为．