Question

18．如图，在平面直角坐标系中，矩形OABC的边OA，OC分别在两坐标轴的正半轴上，B点的坐标为（4，3），平行于对角线AC的一条直线m从原点O出发沿x轴正半轴方向以每秒1个单位的速度运动，直线与矩形OABC的两边分别交于点M，N，设直线的运动时间为t（秒），△OMN的面积为y，则下图哪个曲线能够最准确反映y与t之间的函数关系（　　）

• A．
• B．
• C．
• D．

Answer 1

分析 分两种情形①如图1中，当0＜t≤4时，②如图2中，当4＜t≤8时，分别求出y与t的函数关系式即可解决问题．

解答 解：如图1中，当0＜t≤4时，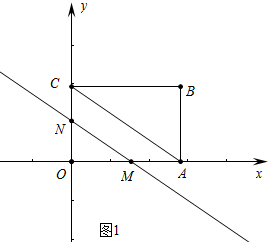

∵MN∥CA，
∴OM：OA=ON：OC，
∴OM：ON=OA：OC=4：3，
∴OM=t，ON=$\frac{3}{4}$t，
∴y=$\frac{1}{2}$•OM•ON=$\frac{3}{8}$t²．
如图2中，当4＜t≤8时，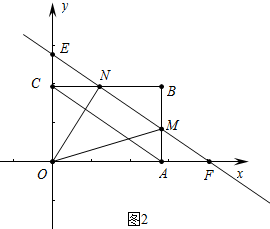

y=S_△EOF-S_△EON-S_△OFM=$\frac{3}{8}$t²-$\frac{1}{2}$•$\frac{3}{4}$t•（t-4）-$\frac{1}{2}$•t•$\frac{3}{4}$（t-4）=-$\frac{3}{8}$t²+3t．
综上所述y=$\left\{\begin{array}{l}{\frac{3}{8}{t}^{2}}&{（0＜t≤4）}\\{-\frac{3}{8}{t}^{2}+3t}&{（4＜t≤8）}\end{array}\right.$，
故选D．

点评 本题考查动点问题函数图象、矩形的性质．三角形的面积等知识，解题的关键是学会分类讨论，求出分段函数的解析式，属于中考常考题型．