题目内容
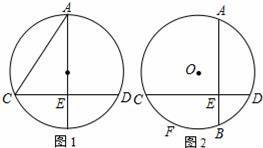
用火柴棍按下列方式摆图形,第1个图形用了4根火柴棍,第2个图形用了10根火柴棍,第3个图形用了18根火柴棍.依照此规律,若第n个图形用了88根火柴棍,则n的值为( )

A.6 B.7 C.8 D.9
C【考点】规律型:图形的变化类.
【分析】根据图形中火柴棒的个数得出变化规律得出第n个图形火柴棒为:n(n+3)根,进而求出n的值即可.
【解答】解:∵第一个图形火柴棒为:1×(1+3)=4根;
第二个图形火柴棒为:2×(2+3)=10根;
第三个图形火柴棒为:3×(3+3)=18根;
第四个图形火柴棒为:4×(4+3)=28根;
…
∴第n个图形火柴棒为:n(n+3)根,
∵88=n(n+3).
∴n的值为8.
故选:C.
【点评】此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
某地连续九天的最高气温统计如下表:
| 最高气温(℃) | 22 | 23 | 24 | 25 |
| 天数 | 1 | 2 | 2 | 4 |
则这组数据的中位数与众数分别是( )
A.24,25 B.24.5,25 C.25,24 D.23.5,24
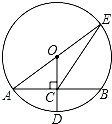

 (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).