题目内容
若a2+2ab-35b2=0（ab≠0），求
+
的值．
| a |
| b |
| b |
| a |
考点：解一元二次方程-因式分解法,分式的化简求值
专题：
分析：先分解因式，求出a=-7b或5b，再分别代入求出即可．
解答：解：∵ab≠0，
∴a≠0，b≠0，
∴a2+2ab-35b2=0，
∴（a+7b）（a-5b）=0，
∴a+7b=0，a-5b=0，
∴a=-7b或5b，
当a=-7b时，
+
=-7-
=-7
；
当a=5b时，
+
=5+
=5
．
∴a≠0，b≠0，
∴a2+2ab-35b2=0，
∴（a+7b）（a-5b）=0，
∴a+7b=0，a-5b=0，
∴a=-7b或5b，
当a=-7b时，
| a |
| b |
| b |
| a |
| 1 |
| 7 |
| 1 |
| 7 |
当a=5b时，
| a |
| b |
| b |
| a |
| 1 |
| 5 |
| 1 |
| 5 |
点评：本题考查了因式分解，解一元二次方程，分式的混合运算的应用，主要考查学生的计算能力．
练习册系列答案
阶梯计算系列答案
相关题目
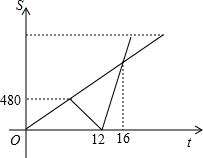如图反映的是甲、乙两人以每分钟80米的速度从公司出发步行到火车站乘车的过程．在去火车站的途中，甲突然发现忘带预购的火车票，于是立刻以同样的速度返回公司，然后乘出租车赶往火车站，途中与乙相遇后，带上乙一同到火车站（忽略停顿所需时间），结果到火车站的时间比预计步行到火车站的时间早到了3分钟．