题目内容
14. 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,求AH的长.
如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,求AH的长.
分析 根据面积的差得出a+b的值,再利用a-b=2,解得a,b的值代入即可.
解答 解:∵AB=10,EF=2,
∴大正方形的面积是100,小正方形的面积是4,
∴四个直角三角形面积和为100-4=96,
设AE=a,DE=b,则4×$\frac{1}{2}$ab=96,
∴2ab=96,a2+b2=100,
∴(a+b)2=a2+b2+2ab=100+96=196,
∴a+b=14,
∵a-b=2,
解得:a=8,b=6,
∴AE=8,DE=6,
∴AH=8-2=6.
点评 此题考查勾股定理的证明,关键是应用直角三角形中勾股定理的运用解得ab的值.

练习册系列答案
相关题目
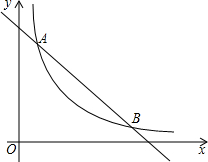 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$与一次函数y=-x+b交于点A(1,6-k),B(m,1).
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$与一次函数y=-x+b交于点A(1,6-k),B(m,1).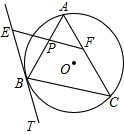 如图,△ABC是⊙O的内接三角形,BT是⊙O的切线,P是线段AB上一点,经过P作BC的平行线与BT交于E点,与AC交于F点.
如图,△ABC是⊙O的内接三角形,BT是⊙O的切线,P是线段AB上一点,经过P作BC的平行线与BT交于E点,与AC交于F点. 如图,点P是等腰Rt△ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设点D为BC中点,求证:△DEF是等腰直角三角形.
如图,点P是等腰Rt△ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设点D为BC中点,求证:△DEF是等腰直角三角形.