题目内容
若二次函数y=kx2-(2k+1)x+k与x轴有两个交点.
(1)求k的取值范围;
(2)若A(x1,0),B(x2,0)是二次函数与x轴的交点且满足x12-x22=0,求k的值.
解:(1)∵函数为二次函数,
∴k≠0,
∵二次函数y=kx2-(2k+1)x+k与x轴有两个交点,
∴△=(2k+1)2-4k×k>0,
∴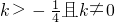 ;
;
(2)∵A(x1,0),B(x2,0)是二次函数与x轴的交点,
∴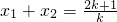 ,
,
而x12-x22=0,
∴x1=x2或x1+x2=0
当x1=x2时△=0, ,
,
当x1+x2=0时 ,
,
∴ .
.
分析:(1)由题意二次函数y=kx2-(2k+1)x+k与x轴有两个交点,可知判别式△>0,从而求出k的范围;
(2)已知函数的解析式,根据根与系数的关系,求出两根之和与两根之积,再根据x12-x22=0,求出k值.
点评:此题主要考查一元二次方程与函数的关系,函数与x轴的交点的横坐标就是方程的根.
∴k≠0,
∵二次函数y=kx2-(2k+1)x+k与x轴有两个交点,
∴△=(2k+1)2-4k×k>0,
∴
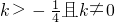 ;
;(2)∵A(x1,0),B(x2,0)是二次函数与x轴的交点,
∴
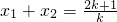 ,
,而x12-x22=0,
∴x1=x2或x1+x2=0
当x1=x2时△=0,
 ,
,当x1+x2=0时
 ,
,∴
 .
.分析:(1)由题意二次函数y=kx2-(2k+1)x+k与x轴有两个交点,可知判别式△>0,从而求出k的范围;
(2)已知函数的解析式,根据根与系数的关系,求出两根之和与两根之积,再根据x12-x22=0,求出k值.
点评:此题主要考查一元二次方程与函数的关系,函数与x轴的交点的横坐标就是方程的根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目