题目内容
 如图,在平面直角坐标系中,四边形ABOC是菱形,点B在y轴的正半轴上,点A在反比例函数y=
如图,在平面直角坐标系中,四边形ABOC是菱形,点B在y轴的正半轴上,点A在反比例函数y=| k |
| x |
(1)填空:菱形ABOC的周长为
(2)若将菱形ABOC向右平移,使菱形的某个顶点落在反比例函数y=
| k |
| x |
考点:菱形的性质,反比例函数图象上点的坐标特征,坐标与图形变化-平移
专题:
分析:(1)由点C的坐标,可求出OC的长,进而求出菱形ABOC的周长;
(2)由菱形的性质易求点A的坐标,进而可求出反比例函数的解析式,再分两种情况讨论即可求出菱形ABOC平移的距离
(2)由菱形的性质易求点A的坐标,进而可求出反比例函数的解析式,再分两种情况讨论即可求出菱形ABOC平移的距离
解答:解:(1)∵点C的坐标为(4,3),
∴OC=
=5,
∴菱形ABOC的周长为4×5=20,
故答案为:20;
(2)由已知易得点A的坐标为(4,8),
∴k=xy=4×8=32.
∴y=
.
①当点C′落在反比例函数y=
(x>0)的图象上时.
设点C′的坐标为(x,3),则3=
,x=
,
∴EE′=OE′-OE=
-4=
,即菱形ABCD平移的距离为
.
②当点B′落在反比例函数y=
(x>0)的图象上时,平移后的点坐标为(
,5);
∴菱形ABOC平移的距离为
;
综上所述,菱形ABCD平移的距离为
或
.
∴OC=
| 32+42 |
∴菱形ABOC的周长为4×5=20,
故答案为:20;
(2)由已知易得点A的坐标为(4,8),
∴k=xy=4×8=32.
∴y=
| 32 |
| x |
①当点C′落在反比例函数y=
| 32 |
| x |
设点C′的坐标为(x,3),则3=
| 32 |
| x |
| 32 |
| 3 |
∴EE′=OE′-OE=
| 32 |
| 3 |
| 20 |
| 3 |
| 20 |
| 3 |
②当点B′落在反比例函数y=
| 32 |
| x |
| 32 |
| 5 |
∴菱形ABOC平移的距离为
| 32 |
| 5 |
综上所述,菱形ABCD平移的距离为
| 20 |
| 3 |
| 32 |
| 5 |
点评:本题主要考查菱形的性质及反比例函数的比例系数k的几何意义.反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知点A(2,y1)和点B(m,y2)是抛物线y=x2-2x上两点,且y2>y1,则m的取值范围是( )
| A、m>2 |
| B、m≤0或m≥2 |
| C、0<m<2 |
| D、m<0或m>2 |
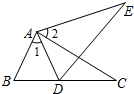 如图,在△ABC和△ADE中,B、D、C三点在同一直线上.有以下四个条件:
如图,在△ABC和△ADE中,B、D、C三点在同一直线上.有以下四个条件: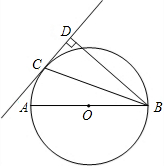 如图,点C是以AB为直径的⊙O上的一点,BD与过点C的切线互相垂直,垂足为点D.
如图,点C是以AB为直径的⊙O上的一点,BD与过点C的切线互相垂直,垂足为点D.