题目内容
13.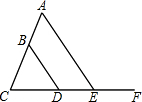 如图,在△BCD中,BC=4,BD=5,
如图,在△BCD中,BC=4,BD=5,(1)求CD的取值范围;
(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
分析 (1)利用三角形三边关系得出DC的取值范围即可;
(2)利用平行线的性质得出∠AEC的度数,再利用三角形内角和定理得出答案.
解答 解:(1)∵在△BCD中,BC=4,BD=5,
∴1<DC<9;
(2)∵AE∥BD,∠BDE=125°,
∴∠AEC=55°,
又∵∠A=55°,
∴∠C=70°.
点评 此题主要考查了三角形三边关系以及平行线的性质,得出∠AEC的度数是解题关键.

练习册系列答案
相关题目
9.一天晚上,小丽在清洗两只颜色分别为粉色和白色的有盖茶杯时,突然停电了,小丽只好把杯盖和茶杯随机搭配在一起,则其颜色搭配一致的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
1.下列各式中,不能用平方差公式计算的是( )
| A. | (-2x-y)(2x-y) | B. | (-2x+y)(-2x-y) | C. | (2x+y)(-2x+y) | D. | (2x-y)(-2x+y) |
2.有一个三角形的两边是6cm和8cm,要使这个三角形为直角三角形,则第三边的长为( )
| A. | 10cm | B. | $2\sqrt{7}$cm | C. | 10cm或2$\sqrt{7}$cm | D. | 4cm |
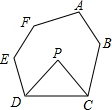 如图,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠DCB,则∠P与∠A+∠B+∠E+∠F的数量关系可表示为∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°.
如图,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠DCB,则∠P与∠A+∠B+∠E+∠F的数量关系可表示为∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°.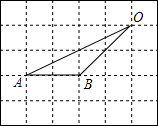 如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠OAB的正弦值是$\frac{\sqrt{5}}{5}$.
如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠OAB的正弦值是$\frac{\sqrt{5}}{5}$.