题目内容
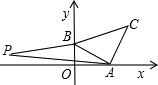 如图,直线y=-
如图,直线y=-| 3 |
| 4 |
(1)求A,B两点的坐标及△ABC的面积;
(2)在第二象限内有一点P(a,1).
①试用含a的代数式表示△ABP的面积;
②若S△ABP=S△ABC,求点P的坐标.
考点:一次函数综合题
专题:
分析:(1)由已知直线y=-
x+3分别令y=0、x=0即可求出A、B的坐标;
(2)连接PO,①分别求得S△AOP=2,S△BOP=-
a,S△AOB=6,根据S△ABP=S△BOP+S△AOB-S△AOP即可求得;②再利用S△ABP=S△ABC建立含a的方程,通过解方程求得答案.
| 3 |
| 4 |
(2)连接PO,①分别求得S△AOP=2,S△BOP=-
| 3 |
| 2 |
解答:解:(1)∵直线y=-
x+3与x轴y轴分别交于点A,B,
令y=0,则0=-
x+3,解得x=4,
∴A(4,0),
令x=0,则y=3,
∴B(0,3),
∴AB=
=5,
∵等腰Rt△ABC中,∠BAC=90°,
∴S△ABC=
×5×5=
;
(2)连接PO,
①∵P(a,1).
∴S△AOP=
OA×1=
×4×1=2,S△BOP=
OB×(-a)=-
a,
∴S△ABP=S△BOP+S△AOB-S△AOP=-
a+
×3×4-2=-
a+4;
②∵S△ABP=S△ABC,
∴-
a+4=
,解得a=-
∴P(-
,1).
| 3 |
| 4 |
令y=0,则0=-
| 3 |
| 4 |
∴A(4,0),
令x=0,则y=3,
∴B(0,3),
∴AB=
| OA2+OB2 |
∵等腰Rt△ABC中,∠BAC=90°,
∴S△ABC=
| 1 |
| 2 |
| 25 |
| 2 |
(2)连接PO,

①∵P(a,1).
∴S△AOP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴S△ABP=S△BOP+S△AOB-S△AOP=-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
②∵S△ABP=S△ABC,
∴-
| 3 |
| 2 |
| 25 |
| 2 |
| 17 |
| 3 |
∴P(-
| 17 |
| 3 |
点评:本题考查了一次函数的综合应用;解函数图象与面积结合的问题,要把相关三角形用边落在坐标轴的其他三角形面积来表示,这样面积与坐标就建立了联系;把S△ABP表示成有边落在坐标轴上的三角形面积和、差是正确解答本题的关键.

练习册系列答案
相关题目
下列运算正确的是( )
| A、x2•x3=x5 |
| B、x2+x2=2x4 |
| C、(-2x2)4=16x6 |
| D、(x+3y)(x-3y)=x2-3y2 |
在数轴上与-3距离4个单位的点表示的数是( )
| A、-1 | B、-1和7 |
| C、1 | D、1和-7 |
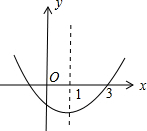 如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,且图象经过点(3,0),下列结论中,正确的是
如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,且图象经过点(3,0),下列结论中,正确的是


