题目内容
10.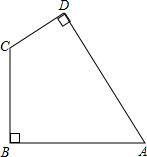 (1)如图,作出四边形ABCD的位似图形A′B′C′D′,使四边形ABCD与四边形A′B′C′D′的相似比为2:1;
(1)如图,作出四边形ABCD的位似图形A′B′C′D′,使四边形ABCD与四边形A′B′C′D′的相似比为2:1;(2)若已知AB=2,BC=$\sqrt{3}$,∠A=60°,AB⊥BC,CD⊥DA,求四边形A′B′C′D′的面积.
分析 (1)连结AC、BD,它们相交于点O,再分别取OA、OB、OC、OD的中点A′、B′、C′、D′,则四边形ABCD与四边形A′B′C′D′的相似比为2:1;
(2)延长AB和DC,它们相交于点E,如图,先利用互余计算出∠E=30°,再根据含30度的直角三角形三边的关系,在Rt△BCE中可计算出CE=2BC=2$\sqrt{3}$,BE=$\sqrt{3}$BC=3,在Rt△ADE中可计算出AD=$\frac{1}{2}$AE=$\frac{5}{2}$,DE=$\sqrt{3}$AD=$\frac{5\sqrt{3}}{2}$,则可利用S四边形ABCD=S△ADE-S△BCE计算出四边形ABCD的面积,然后根据相似的性质可计算出四边形A′B′C′D′的面积.
解答 解:(1)如图,四边形A′B′C′D′为所求;
(2)延长AB和DC,它们相交于点E,如图,
∵AB⊥BC,CD⊥DA,
∴∠ADE=∠EBC=90°,
∵∠A=60°,
∴∠E=30°,
在Rt△BCE中,CE=2BC=2$\sqrt{3}$,BE=$\sqrt{3}$BC=3,
∴AE=BE+AB=5,
在Rt△ADE中,AD=$\frac{1}{2}$AE=$\frac{5}{2}$,DE=$\sqrt{3}$AD=$\frac{5\sqrt{3}}{2}$,
∴S四边形ABCD=S△ADE-S△BCE=$\frac{1}{2}$×$\frac{5}{2}$×$\frac{5\sqrt{3}}{2}$-$\frac{1}{2}$×$\sqrt{3}$×3=$\frac{13\sqrt{3}}{8}$,
∵四边形ABCD与四边形A′B′C′D′的相似比为2:1,
∴$\frac{{S}_{四边形ABCD}}{{S}_{四边形A′B′C′D′}}$=22,
∴S四边形A′B′C′D′=$\frac{1}{4}$×$\frac{13\sqrt{3}}{8}$=$\frac{13\sqrt{3}}{32}$.
点评 本题考查了作图-位似变换:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了相似的性质和含30度的直角三角形三边的关系.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案| A. | -(-2)与-(+2) | B. | +(-5)与-|-5| | C. | |-3|与|+3| | D. | |a|与|-a| |
 如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )
如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )| A. | $\frac{20}{sin37°}$ | B. | 20tan37° | C. | $\frac{20}{tan37°}$ | D. | 20sin37° |
| A. | $\frac{8}{3}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | $\frac{1}{16}$ |
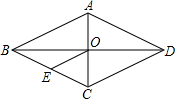 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC中点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC中点E,AD=6cm,则OE的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
| A. | |-2|3=|2|3 | B. | (-2)2=22 | C. | (-2)3=-23 | D. | (-2)4=-24 |
 如图,点A,B分别是直线l异侧的两个点,请你在l上找到一个点,使得这个点到点A,点B的距离的和最短.
如图,点A,B分别是直线l异侧的两个点,请你在l上找到一个点,使得这个点到点A,点B的距离的和最短.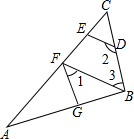 如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°.
如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°.