题目内容
1.关于x的方程kx2+(k+2)x+$\frac{k}{4}$=0有实数根.(1)求k的取值范围.
(2)若x1,x2是方程kx2+(k+2)x+$\frac{k}{4}$=0的两个实数根,且满足kx1-12x1x2=-kx2,求k.
分析 (1)分为两种情况:当k-1=0时和当k-1≠0时,求出即可;
(2)利用根与系数的关系得出x1+x2=-$\frac{k+2}{k}$,x1x2=$\frac{1}{4}$,代入kx1-12x1x2=-kx2求得k的数值即可.
解答 解:(1)当k=0时,方程为2x+$\frac{1}{2}$=0,方程有实数根;
当k≠0时,△=(k+2)2-4•k•$\frac{k}{4}$≥0时,即k≥-1,方程有实数根,
综合上述:k的取值范围是k≥-1;
(2)∵x1,x2是方程kx2+(k+2)x+$\frac{k}{4}$=0的两个实数根,
∴x1+x2=-$\frac{k+2}{k}$,x1x2=$\frac{1}{4}$,
∴kx1-12x1x2=-kx2,
k(x1+x2)-12x1x2=0,
k+2-3=0,
解得:k=1.
点评 本题考查了根与系数的关系及根的判别式,难度适中,关键是掌握x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知点(-2,1)在双曲线y=$\frac{k}{x}$上,则下列各点一定在该双曲线上的是( )
| A. | (1,-2) | B. | (-2,-1) | C. | (2,1) | D. | (1,2) |
9.数轴上到原点的距离是3.5的数是( )
| A. | 3.5 | B. | -3.5 | C. | 3.5或-3.5 | D. | 7 |
6.下列计算结果不正确的是( )
| A. | 4+(-2)=2 | B. | -2-(-1.5)=-0.5 | C. | -(-4)+4=8 | D. | |-6|+|2|=4 |
11.在下面的四个有理数中,最小的是( )
| A. | -1 | B. | 0 | C. | 1 | D. | -2 |
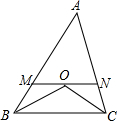 如图,△ABC中,AB=8,AC=6,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为14.
如图,△ABC中,AB=8,AC=6,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为14.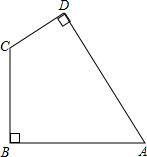 (1)如图,作出四边形ABCD的位似图形A′B′C′D′,使四边形ABCD与四边形A′B′C′D′的相似比为2:1;
(1)如图,作出四边形ABCD的位似图形A′B′C′D′,使四边形ABCD与四边形A′B′C′D′的相似比为2:1;