题目内容
 如图,四边形AOBC是矩形,O为原点,A、B的坐标分别为(0,4)、(6,0),F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=
如图,四边形AOBC是矩形,O为原点,A、B的坐标分别为(0,4)、(6,0),F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=| k |
| x |
(1)当k=2时,写出点E、F的坐标;
(2)求
| CE |
| CF |
(3)是否存在这样的点F,使得将△CEF沿EF对折后,C点恰好落在OB上?若存在,求出此时点F的坐标;若不存在,请说明理由.
考点:反比例函数综合题
专题:
分析:(1)根据题意可知E的纵坐标为4,F的横坐标为6,分别代入y=
,即可求得E、F的坐标;
(2)根据反比例函数的性质得出,xy=k,即可得出AE•AO=BF•BO,从而得出
=
,进而求得
=
=
=
;
(3)设折叠之后C点在OB上的对称点为C',连接C'E、C'F,过E作EG垂直于OB于点G,则根据折叠性质、相似三角形、勾股定理得出即可.
| 2 |
| x |
(2)根据反比例函数的性质得出,xy=k,即可得出AE•AO=BF•BO,从而得出
| AE |
| AC |
| BF |
| BC |
| CE |
| CF |
| AC |
| BC |
| 6 |
| 4 |
| 3 |
| 2 |
(3)设折叠之后C点在OB上的对称点为C',连接C'E、C'F,过E作EG垂直于OB于点G,则根据折叠性质、相似三角形、勾股定理得出即可.
解答:解:(1)当k=2时,则y=
,
∵反比例函数y=
的图象经过点E、F,
∵A、B的坐标分别为(0,4)、(6,0),
∴E的纵坐标为4,F的横坐标为6,
∴E(
,4),F(6,
);
(2)∵根据反比例函数的性质得出,xy=k,
∴AE•AO=BF•BO,
∴
=
,
∵AC=OB,BC=AO,
∴
=
,
∴EF∥BC,
∴
=
,
∴
=
=
=
;
(3)设存在这样的点F,将△CEF沿EF对折后,C点恰好落在OB边上的C'点,
过点E作EG⊥OB,垂足为G.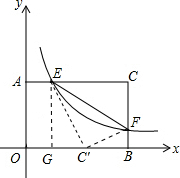
由题意得:EG=AO=4,
把y=4代入y=
得:x=
k,把x=6代入y=
得:y=
k,
∴EC'=EC=6-
k,C′F=CF=4-
k,
∵∠EC'G+∠FC'B=∠FC'B+∠C'FB=90°,
∴∠EC'G=∠C'FB.
又∵∠EGC'=∠C'BF=90°,
∴△EC'G∽△C'FB.
∴EG:C'B=EC':C'F,
∴4:C'B=(6-
k):(4-
k)=[3(2-
k)]:[2(2-
k)],
∴C'B=
,
∵C'B2+BF2=C'F2,
∴(
)2+(
k)2=(4-
k)2,
解得k=
,
∴BF=
=
,
∴存在符合条件的点F,它的坐标为(6,
).
| 2 |
| x |
∵反比例函数y=
| 2 |
| x |
∵A、B的坐标分别为(0,4)、(6,0),
∴E的纵坐标为4,F的横坐标为6,
∴E(
| 1 |
| 2 |
| 1 |
| 3 |
(2)∵根据反比例函数的性质得出,xy=k,
∴AE•AO=BF•BO,
∴
| AE |
| OB |
| BF |
| AO |
∵AC=OB,BC=AO,
∴
| AE |
| AC |
| BF |
| BC |
∴EF∥BC,
∴
| EC |
| AC |
| CF |
| BC |
∴
| CE |
| CF |
| AC |
| BC |
| 6 |
| 4 |
| 3 |
| 2 |
(3)设存在这样的点F,将△CEF沿EF对折后,C点恰好落在OB边上的C'点,
过点E作EG⊥OB,垂足为G.

由题意得:EG=AO=4,
把y=4代入y=
| k |
| x |
| 1 |
| 4 |
| k |
| x |
| 1 |
| 6 |
∴EC'=EC=6-
| 1 |
| 4 |
| 1 |
| 6 |
∵∠EC'G+∠FC'B=∠FC'B+∠C'FB=90°,
∴∠EC'G=∠C'FB.
又∵∠EGC'=∠C'BF=90°,
∴△EC'G∽△C'FB.
∴EG:C'B=EC':C'F,
∴4:C'B=(6-
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 12 |
∴C'B=
| 8 |
| 3 |
∵C'B2+BF2=C'F2,
∴(
| 8 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
解得k=
| 20 |
| 3 |
∴BF=
| k |
| 6 |
| 10 |
| 9 |
∴存在符合条件的点F,它的坐标为(6,
| 10 |
| 9 |
点评:此题主要考查了反比例函数的性质以及相似三角形的判定与性质,特别注意利用数形结合以及利用相似三角形的性质是这部分考查的重点也是难点.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
-9的绝对值是( )
| A、-9 | ||
| B、9 | ||
C、
| ||
| D、以上答案都不是 |
 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)的对称轴是直线x= 如图所示,一个无盖纸盒的长、宽、高都是8cm.
如图所示,一个无盖纸盒的长、宽、高都是8cm. 如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为20m,求这栋楼的高度.(结果保留根号)
如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为20m,求这栋楼的高度.(结果保留根号)