题目内容
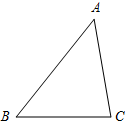 补全图形并写出下列命题的已知、求证,完成证明过程.
补全图形并写出下列命题的已知、求证,完成证明过程.命题:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图,
求证:
证明:
考点:三角形中位线定理
专题:证明题
分析:根据命题找出题设和结论,然后根据题设写出已知:在△ABC中,点D、E分别是AB,AC的中点,根据结论写出求证:DE∥BC,DE=
BC.首先延长DE到点F,使EF=DE,连接CF,证明△AED≌△CEF,可得AD=CF,∠A=∠ECF,进而可证出AB∥CF,然后再证明四边形BDFC是平行四边形,根据平行四边形的性质可得DE∥BC,DF=BC,进而可证出DE=
DF=
BC.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 已知:如图,在△ABC中,点D、E分别是AB,AC的中点.
已知:如图,在△ABC中,点D、E分别是AB,AC的中点.
求证:DE∥BC,DE=
BC.
证明:延长DE到点F,使EF=DE,连接CF.
∵点E是AC中点,
∴AE=EC.
∵在△AED和△CEF中
,
∴△AED≌△CEF(SAS).
∴AD=CF,∠A=∠ECF,
∴AB∥CF.
∵点D是AB中点,
∴AD=BD.
∴BD=CF.
∴四边形BDFC是平行四边形.
∴DE∥BC,DF=BC.
∴DE=
DF=
BC.
 已知:如图,在△ABC中,点D、E分别是AB,AC的中点.
已知:如图,在△ABC中,点D、E分别是AB,AC的中点.求证:DE∥BC,DE=
| 1 |
| 2 |
证明:延长DE到点F,使EF=DE,连接CF.
∵点E是AC中点,
∴AE=EC.
∵在△AED和△CEF中
|
∴△AED≌△CEF(SAS).
∴AD=CF,∠A=∠ECF,
∴AB∥CF.
∵点D是AB中点,
∴AD=BD.
∴BD=CF.
∴四边形BDFC是平行四边形.
∴DE∥BC,DF=BC.
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了三角形的中位线,以及平行四边形的判定与性质,关键是证明四边形BDFC是平行四边形.

练习册系列答案
相关题目
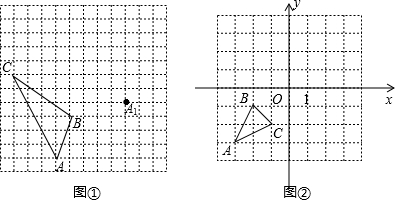
 分别画下图几何体的三视图.
分别画下图几何体的三视图.