题目内容
解方程:
(1)(2x-3)2=(x-2)2;
(2)(x+1)(x-1)+2(x+3)=8.
(1)(2x-3)2=(x-2)2;
(2)(x+1)(x-1)+2(x+3)=8.
考点:解一元二次方程-因式分解法
专题:
分析:(1)移项后用十字相乘法解答;
(2)化为一般式用公式法解答.
(2)化为一般式用公式法解答.
解答:(1)解:原方程可变形为:
(2x-3+x-2)(2x-3-x+2)=0,
(3x-5)(x-1)=0,
3x-5=0或x-1=0,
∴x1=
,x2=1.
(2)解:原方程可化为:
x2+2x-3=0,
这里a=1,b=2,c=-3,
∵b2-4ac=22-4×1×(-3)=4+12=16>0,
∴x=
=
=-1±2,
∴x1=1,x2=-3.
(2x-3+x-2)(2x-3-x+2)=0,
(3x-5)(x-1)=0,
3x-5=0或x-1=0,
∴x1=
| 5 |
| 3 |
(2)解:原方程可化为:
x2+2x-3=0,
这里a=1,b=2,c=-3,
∵b2-4ac=22-4×1×(-3)=4+12=16>0,
∴x=
-2±
| ||
| 2×1 |
| -2±4 |
| 2 |
∴x1=1,x2=-3.
点评:本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
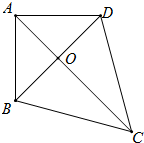 如图,BA⊥AD,∠ADB=∠ABD=∠DAO,∠DBC=60°,∠DCO=∠BCO.
如图,BA⊥AD,∠ADB=∠ABD=∠DAO,∠DBC=60°,∠DCO=∠BCO. 补全图形并写出下列命题的已知、求证,完成证明过程.
补全图形并写出下列命题的已知、求证,完成证明过程. 在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=5km,BC=3km,CD=3km,DE=2km,EF=1km,他们全部乘出租车上、下班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算).
在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=5km,BC=3km,CD=3km,DE=2km,EF=1km,他们全部乘出租车上、下班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算).