题目内容
 如图,已知以点O为公共圆心的两个同心圆,大圆的弦AB交小圆于C,D.
如图,已知以点O为公共圆心的两个同心圆,大圆的弦AB交小圆于C,D.(1)求证:AC=DB;
(2)如果AB=6cm,CD=4cm,求圆环的面积.
考点:垂径定理,勾股定理
专题:
分析:(1)首先过点O作OE⊥AB于E,由垂径定理可证得AE=BE,CE=DE,继而可得AC=BD;
(2)首先连接OA,OC,由勾股定理可得:OE2=OA2-AE2,OE2=OC2-CE2,继而可得OA2-OC2=5,则可求得圆环的面积
(2)首先连接OA,OC,由勾股定理可得:OE2=OA2-AE2,OE2=OC2-CE2,继而可得OA2-OC2=5,则可求得圆环的面积
解答: 解:(1)过点O作OE⊥AB于E,
解:(1)过点O作OE⊥AB于E,
∴AE=BE,CE=DE,
∴AE-CE=BE-DE,
∴AC=BD;
(2)连接OA,OC,
在Rt△AOE与Rt△OCE中:OE2=OA2-AE2,OE2=OC2-CE2,
∴OA2-AE2=OC2-CE2,
∴OA2-OC2=AE2-CE2,
∵AB=6cm,CD=4cm,
∴AE=3cm,CE=2cm,
∴OA2-OC2=5,
∴圆环的面积为:πOA2-πOC2=π(OA2-OC2)=5π.
 解:(1)过点O作OE⊥AB于E,
解:(1)过点O作OE⊥AB于E,∴AE=BE,CE=DE,
∴AE-CE=BE-DE,
∴AC=BD;
(2)连接OA,OC,
在Rt△AOE与Rt△OCE中:OE2=OA2-AE2,OE2=OC2-CE2,
∴OA2-AE2=OC2-CE2,
∴OA2-OC2=AE2-CE2,
∵AB=6cm,CD=4cm,
∴AE=3cm,CE=2cm,
∴OA2-OC2=5,
∴圆环的面积为:πOA2-πOC2=π(OA2-OC2)=5π.
点评:此题考查了垂径定理与勾股定理的知识.此题难度适中,解题的关键是注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
相关题目

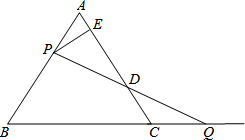 如图,△ABC是边长为12的等边三角形,P是AB上一动点,由A向B运动(与A、B点不重合),Q是BC延长线上一点,与点P同时以相同的速度由C向BC延长线方向运动(Q不与C点重合),过P作PE⊥AC于E,连接PQ交AC于D.
如图,△ABC是边长为12的等边三角形,P是AB上一动点,由A向B运动(与A、B点不重合),Q是BC延长线上一点,与点P同时以相同的速度由C向BC延长线方向运动(Q不与C点重合),过P作PE⊥AC于E,连接PQ交AC于D.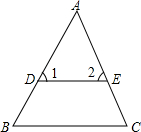 如图,在△ABC中,AB=AC,点D、E分别是AB、AC上的点,且DE∥BC,求证:△ADE是等腰三角形.
如图,在△ABC中,AB=AC,点D、E分别是AB、AC上的点,且DE∥BC,求证:△ADE是等腰三角形.