Question

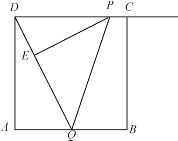
【题目】如图，正方形ABCD，点P为射线DC上的一个动点，点Q为AB的中点，连接PQ，DQ，过点P作PE⊥DQ于点E．

（1）请找出图中一对相似三角形，并证明；

（2）若AB＝4，以点P，E，Q为顶点的三角形与△ADQ相似，试求出DP的长．

Answer 1

【答案】（1）△DPE∽△QDA，证明见解析；（2）DP=2或5

【解析】

（1）由∠ADC＝∠DEP＝∠A＝90可证明△ADQ∽△EPD；

（2）若以点P，E，Q为顶点的三角形与△ADQ相似，有两种情况，当△ADQ∽△EPQ时，设EQ＝x，则EP＝2x，则DE＝2x，由△ADQ∽△EPD可得，可求出x的值，则DP可求出；同理当△ADQ∽△EQP时，设EQ＝2a，则EP＝a，可得，可求出a的值，则DP可求．

（1）△ADQ∽△EPD，证明如下：

∵PE⊥DQ，

∴∠DEP＝∠A＝90，

∵∠ADC＝90，

∴∠ADQ＋∠EDP＝90，∠EDP＋∠DPE＝90，

∴∠ADQ＝∠DPE，

∴△ADQ∽△EPD；

（2）∵AB＝4，点Q为AB的中点，

∴AQ＝BQ＝2，

∴DQ＝，

∵∠PEQ＝∠A＝90，

∴若以点P，E，Q为顶点的三角形与△ADQ相似，有两种情况，

①当△ADQ∽△EPQ时，，

设EQ＝x，则EP＝2x，则DE＝2x，

由（1）知△ADQ∽△EPD，

∴，

∴，

∴x＝

∴DP＝＝5；

②当△ADQ∽△EQP时，设EQ＝2a，则EP＝a，

同理可得，

∴a＝，

DP＝．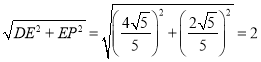

综合以上可得DP长为2或5，使得以点P，E，Q为顶点的三角形与△ADQ相似．