题目内容
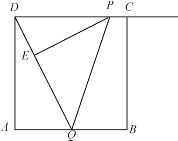
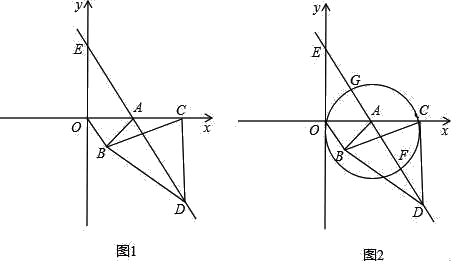
【题目】如图1，在直角坐标系中，点A的坐标为（1，0），以OA为边在第四象限内作等边△AOB，点C为x轴的正半轴上一动点（OC＞1），连接BC，以BC为边在第四象限内作等边△CBD，直线DA交y轴于点E．
（1）试问△OBC与△ABD全等吗？并证明你的结论；
（2）随着点C位置的变化，点E的位置是否会发生变化？若没有变化，求出点E的坐标；若有变化，请说明理由；
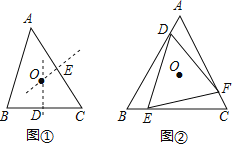
（3）如图2，以OC为直径作圆，与直线DE分别交于点F、G，设AC=m，AF=n，用含n的代数式表示m
【答案】(1)两个三角形全等,理由见解析;（2）见解析;（3）m=
．
【解析】
（1）由等边三角形的性质知，OBA=∠CBD=60°，易得∠OBC=∠ABD，又有OB=AB，BC=BD故有△OBC≌△ABD；
（2）由1知，△OBC≌△ABD∠BAD=∠BOC=60°，可得∠OAE=60°，在Rt△EOA中，有EO=OAtan60°=
，即可求得点E的坐标；
（3）由相交弦定理知1m=nAG，即AG=
，由切割线定理知，OE2=EGEF，在Rt△EOA中，由勾股定理知，AE=
=2，故建立方程：（）2=（2-）（2+n），就可求得m与n关系．
（1）两个三角形全等．
∵△AOB、△CBD都是等边三角形，
∴OBA=∠CBD=60°，
∴∠OBA+∠ABC=∠CBD+∠ABC，
即∠OBC=∠ABD；
∵OB=AB，BC=BD，
△OBC≌△ABD；
（2）点E位置不变．
∵△OBC≌△ABD，
∴∠BAD=∠BOC=60°，
∠OAE=180°﹣60°﹣60°=60°，
在Rt△EOA中，EO=OAtan60°=，
或∠AEO=30°，得AE=2，
∴OE=，
∴点E的坐标为（0，）；
（3）∵AC=m，AF=n，由相交弦定理知1m=nAG，即AG=，
又∵OC是直径，
∴OE是圆的切线，OE2=EGEF，
在Rt△EOA中，AE==2，
（）2=（2﹣）（2+n）
即2n2+n﹣2m﹣mn=0
解得m=．
