题目内容
【题目】已知函数![]() (
(![]() 为常数)
为常数)
(1)该函数的图像与![]() 轴公共点的个数是( )
轴公共点的个数是( )
A.0 B.1 C.2 D.1或2
(2)求证:不论![]() 为何值,该函数的图像的顶点都在函数
为何值,该函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)当![]() 时,求该函数的图像的顶点纵坐标的取值范围.
时,求该函数的图像的顶点纵坐标的取值范围.
【答案】(1)D(2)证明见解析(3)![]()
【解析】
试题分析:(1)根据根的判别式可判断;
(2)先利用配方法求出函数的顶点坐标,然后代入![]() 可得证;
可得证;
(3)设函数![]()
![]() ,然后分类讨论即可.
,然后分类讨论即可.
试题解析:(1)![]() .
.
(2)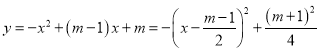 ,
,
所以该函数的图像的顶点坐标为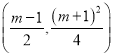 .
.
把![]()
![]() 代入
代入![]() ,得
,得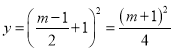 .
.
因此,不论![]() 为何值,该函数的图像的顶点都在函数
为何值,该函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)设函数![]()
![]() .
.
当![]() 时,
时,![]() 有最小值0.
有最小值0.
当![]() 时,
时,![]() 随
随![]() 的增大而减小;当
的增大而减小;当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.
又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此,当![]() 时,该函数的的图像的顶点纵坐标的取值范围是
时,该函数的的图像的顶点纵坐标的取值范围是![]() .
.

练习册系列答案
相关题目