Question

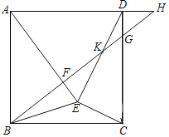
【题目】在等边三角形ABC中，点D，E分别在BC，AC上，且DC=AE，AD与BE交于点P，连接PC.

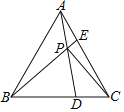
(1)证明：ΔABE≌ΔCAD.

(2)若CE=CP，求证∠CPD=∠PBD.

(3)在(2)的条件下，证明：点D是BC的黄金分割点.

Answer 1

【答案】（1）见解析；（2）见解析；（3）见解析

【解析】

（1）因为△ABC是等边三角形，所以AB=AC，∠BAE=∠ACD=60°，又AE=CD，即可证明ΔABE≌ΔCAD；

（2）设则由等边对等角可得可得以及，故；

（3）可证可得，故由于可得，根据黄金分割点可证点是的黄金分割点；

证明：

(1) ∵△ABC是等边三角形，

∴AB=AC，∠BAE=∠ACD=60°，

在ΔABE与ΔCDA中，AB=AC，∠BAE=∠ACD=60°，AE=CD，

∴△AEB≌△CDA；

（2）由（1）知，

则，

设，

则，

∵，

∴，

∴，

又，

∴；

（3）在和中，

，，

∴，

∴，

∴，

又，

∴，

∴点是的黄金分割点；