Question

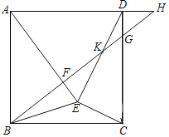
【题目】如图，在边长为4正方形ABCD中，以AB为腰向正方形内部作等腰△ABE，点G在CD上，且CG＝3DG．连接BG并延长，与AE交于点F，与AD延长线交于点H．连接DE交BH于点K．若AE2＝BFBH，则S△CDE＝__．

Answer 1

【答案】

【解析】

根据题意作EM⊥AB于M，EM交CD于N，如图，利用勾股定理计算出BG＝5，再证明△HDG∽△HAB，利用相似比计算出HB＝，再证明△BAF∽△BHA得到∠BFA＝∠BAH＝90°，接着求出BF得到ME＝BF＝，然后计算出EN后利用三角形面积公式计算．

解：作EM⊥AB于M，EM交CD于N，如图，则EN⊥CD，

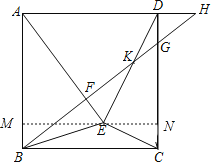
∵CG＝3DG，

∴DG＝1，CG＝3，

在Rt△BCG中，BG＝＝5，

∵DG∥AB，

∴△HDG∽△HAB，

∴＝，即＝，解得HB＝，

∵AE2＝BFBH，而AB＝AE，

∴AB2＝BFBH，即AB：BF＝BH：AB，

而∠ABF＝∠HBA，

∴△BAF∽△BHA，

∴∠BFA＝∠BAH＝90°，

∴BF⊥EM，

∵BF＝＝，

∴ME＝BF＝，

∴EN＝4﹣＝，

∴S△CDE＝×4×＝．

故答案为．