��Ŀ����
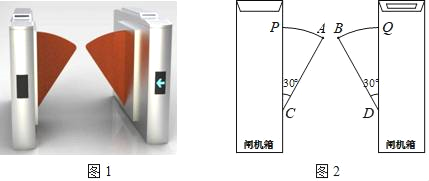
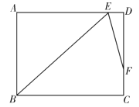
����Ŀ��������һ����λ��![]() �����
�����![]() �������λ�ϵ����ֻ�����ͬ���Ҷ���Ϊ�㣬��ô�������Ϊ����������.��һ����������������������λ�ϵ����ֶԵ�����Եõ�������ͬ������λ����������������λ���ĺ���111���̼�Ϊ
�������λ�ϵ����ֻ�����ͬ���Ҷ���Ϊ�㣬��ô�������Ϊ����������.��һ����������������������λ�ϵ����ֶԵ�����Եõ�������ͬ������λ����������������λ���ĺ���111���̼�Ϊ![]() .����
.����![]() ���Ե���λ��ʮλ�ϵ����ֵõ�213���Ե���λ���λ�ϵ����ֵõ�321���Ե�ʮλ���λ�ϵ����ֵõ�132������������λ���ĺ�
���Ե���λ��ʮλ�ϵ����ֵõ�213���Ե���λ���λ�ϵ����ֵõ�321���Ե�ʮλ���λ�ϵ����ֵõ�132������������λ���ĺ�![]() ��
��![]() ������
������![]() .
.
��1�����㣺![]() ��
��![]() ��
��
��2��С���ڼ���![]() ʱ���ּ��������Ϊ��������С���������е�
ʱ���ּ��������Ϊ��������С���������е�![]() ��Ϊ����������������������ȷ�����жϲ�˵�����ɣ�
��Ϊ����������������������ȷ�����жϲ�˵�����ɣ�
��3����![]() ��
��![]() ��������������������
��������������������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����������������
����������������![]() ʱ����
ʱ����![]() �����ֵ.
�����ֵ.
���𰸡���1��10��12.��2��������ȷ.���ɼ���������3��![]() .
.
��������
��1�����������������Ķ��弴����⣻
��2����![]() ��������λ���ֱַ�Ϊ
��������λ���ֱַ�Ϊ![]() ��
��![]() ��
��![]() �����������������Ķ����г�
�����������������Ķ����г�![]() ������⣻
������⣻
��3������![]() ��
��![]() �����������������õ�
�����������������õ�![]() ��
��![]() ������
������![]() ���x��y��ֵ�������.
���x��y��ֵ�������.
��1��![]() ��
��
![]() .
.
��2��������ȷ.��![]() ��������λ���ֱַ�Ϊ
��������λ���ֱַ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ��
��
![]()
![]() .
.
��Ϊ![]() ��
��![]() ��
��![]() ������������������
������������������![]() ������.
������.
��3����![]() ��
��![]() ����������������
����������������
��![]() ��
��
![]() .
.
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��![]() ������������
������������
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ����������������
����������������![]() ��
��
��![]() ����������������
����������������![]() ��
��
��������������![]() ����
����![]() ����
����![]() ��
��
�� ![]() ��
�� ��
��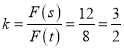 ��
��
��![]() �����ֵΪ
�����ֵΪ![]() .
.